
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%
科目:高中数学 来源: 题型:
【题目】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为![]() ,乙每次投球命中的概率为
,乙每次投球命中的概率为![]() ,且各次投球互不影响.
,且各次投球互不影响.
(1)经过1轮投球,记甲的得分为![]() ,求
,求![]() 的分布列;
的分布列;
(2)若经过![]() 轮投球,用
轮投球,用![]() 表示经过第
表示经过第![]() 轮投球,累计得分,甲的得分高于乙的得分的概率.
轮投球,累计得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机计算可估计得
,经过计算机计算可估计得![]() ,请根据①中
,请根据①中![]() 的值分别写出a,c关于b的表达式,并由此求出数列
的值分别写出a,c关于b的表达式,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多边形ABPCD中(图1),四边形ABCD为长方形,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,现以BC为折痕将
,现以BC为折痕将![]() 折起,使点P在平面ABCD内的射影恰好在AD上(图2).
折起,使点P在平面ABCD内的射影恰好在AD上(图2).
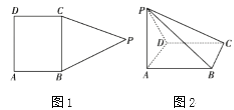
(1)证明:平面![]() 平面PAB;
平面PAB;
(2)若点E在线段PB上,且![]() ,当点Q在线段AD上运动时,求点Q到平面EBC的距离.
,当点Q在线段AD上运动时,求点Q到平面EBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击“新冠肺炎”,全国各地“停课不停学”,各学校都开展了在线课堂,组织学生在线学习,并自主安排时间完成相应作业为了解学生的学习效率,某在线教育平台统计了部分高三备考学生每天完成数学作业所需的平均时间,绘制了如图所示的频率分布直方图.
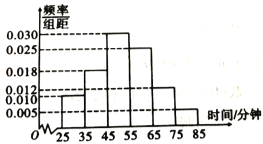
(1)如果学生在完成在线课程后每天平均自主学习时间(完成各科作业及其他自主学习)为![]() 小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到
小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到![]() );
);
(2)以统计的频率作为概率,估计一个高三备考学生每天完成数学作业的平均时间不超过![]() 分钟的概率.
分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】团购已成为时下商家和顾客均非常青睐的一种省钱、高校的消费方式,不少商家同时加入多家团购网.现恰有三个团购网站在![]() 市开展了团购业务,
市开展了团购业务, ![]() 市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
(1)从所调查的50家商家中任选两家,求他们加入团购网站的数量不相等的概率;
(2)从所调查的50家商家中任取两家,用![]() 表示这两家商家参加的团购网站数量之差的绝对值,求随机变量
表示这两家商家参加的团购网站数量之差的绝对值,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)将频率视为概率,现从![]() 市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为
市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为![]() ,试求事件“
,试求事件“![]() ”的概率.
”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音、短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访140位市民进行调查,其中每天玩微信超过6小时的用户称为“微信控”,否则称其为“非微信控”, 调查结果统计如下:
微信控 | 非微信控 | 合计 | |
女性 | 60 | ||
男性 | 30 | ||
合计 | 70 | 140 |
(1)根据以上数据,把表格中的数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
①是否在犯错误的概率不超过0.001的前提下认为“微信控”与“性别”有关;
②已知在被调查的女性“微信控”市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取2人,求至少有1位老师的概率.
附表:![]() 其中
其中![]()
P(K2≥k) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了![]() 件产品作为样本,检测一项质量指标值,若该项质量指标值落在
件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表
内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表![]() 是设备改造后的样本的频数分布表.
是设备改造后的样本的频数分布表.
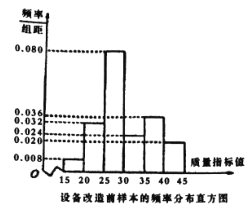
表:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据频率分布直方图和表 提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在![]() 内的定为一等品,每件售价
内的定为一等品,每件售价![]() 元;质量指标值落在
元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价
内的定为二等品,每件售价![]() 元;其它的合格品定为三等品,每件售价
元;其它的合格品定为三等品,每件售价![]() 元.根据表
元.根据表![]() 的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: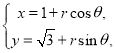 (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
: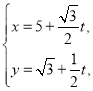 (
(![]() 为参数).若曲线
为参数).若曲线![]() 和
和![]() 相切.
相切.
(1)在以![]() 为极点,
为极点,![]() 轴非负半轴为极轴的极坐标系中,求曲线
轴非负半轴为极轴的极坐标系中,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若点![]() ,
,![]() 为曲线
为曲线![]() 上两动点,且满足
上两动点,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com