【题目】已知四个命题:
①如果向量![]() 与
与![]() 共线,则
共线,则![]() 或
或![]() ;
;
②![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③命题![]() :
:![]() ,
,![]() 的否定是
的否定是![]() :
:![]() ,
,![]() ;
;
④“指数函数![]() 是增函数,而
是增函数,而![]() 是指数函数,所以
是指数函数,所以![]() 是增函数”此三段论大前提错误,但推理形式是正确的.
是增函数”此三段论大前提错误,但推理形式是正确的.
以上命题正确的个数为( )
A.0B.1C.2D.3
参考答案:
【答案】B
【解析】
由向量共线定理可判断①;由充分必要条件的定义可判断②;由特称命题的否定为全称命题,可判断③;由指数函数的单调性可判断④.
①,如果向量![]() 与
与![]() 共线,可得x
共线,可得x![]() y
y![]() ,不一定
,不一定![]() 或
或![]() ,故①错误;
,故①错误;
②,|x|≤3﹣3≤x≤3,x≤3不能推得|x|≤3,但|x|≤3能推得x≤3,
x≤3是|x|≤3的必要不充分条件,故②错误;
③,命题p:x0∈(0,2),![]() 的否定
的否定
是¬p:x∈(0,2),x2﹣2x﹣3≥0,故③错误;
④,“指数函数y=ax是增函数,而![]() 是指数函数,所以
是指数函数,所以![]() 是增函数”
是增函数”
由于a>1时,y=ax为增函数,0<a<1时,y=ax为减函数,此三段论大前提错误,但推理形式是正确的,故④正确.其中正确个数为1.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为
的定义域为 ;
;(1)求实数
 的取值范围;
的取值范围;(2)设实数
 为
为 的最大值,若实数
的最大值,若实数 ,
, ,
, 满足
满足 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
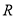 的函数
的函数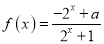 是奇函数
是奇函数(Ⅰ)求
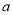 值;
值;(Ⅱ)判断并证明该函数在定义域
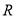 上的单调性;
上的单调性;(Ⅲ)若对任意的
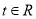 ,不等式
,不等式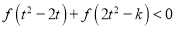 恒成立,求实数
恒成立,求实数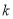 的取值范围;
的取值范围;(Ⅳ)设关于
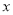 的函数
的函数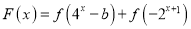 有零点,求实数
有零点,求实数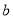 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数
 满足
满足 ,
, 的虚部为2,
的虚部为2,(1)求复数
 ;
;(2)设
 在复平面上对应点分别为
在复平面上对应点分别为 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照我国《机动车交通事故责任强制保险条例》规定,交强险是车主必须为机动车购买的险种,若普通7座以下私家车投保交强险第一年的费用(基准保费)统一为
 元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:交强险浮动因素和浮动费率比率表
投保类型
浮动因素
浮动比率

上一个年度未发生有责任道路交通事故
下浮10%

上两个年度未发生有责任道路交通事故
下浮20%

上三个及以上年度未发生有责任道路交通事故
下浮30%

上一个年度发生一次有责任不涉及死亡的道路交通事故
0%

上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故
上浮10%

上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了研究某一品牌普通7座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车在下一年续保时的情况,统计得到了下面的表格:
类型






数量
20
10
10
20
15
5
(1)根据上述样本数据,估计一辆普通7座以下私家车(车龄已满3年)在下一年续保时,保费高于基准保费的概率;
(2)某销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基准保费的车辆记为事故车.
①若该销售商部门店内现有6辆该品牌二手车(车龄已满3年),其中两辆事故车,四辆非事故车.某顾客在店内随机挑选两辆车,求这两辆车中恰好有一辆事故车的概率;
②以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率.该销售商一次购进120辆(车龄已满三年)该品牌二手车,若购进一辆事故车亏损4000元,一辆非事故车盈利8000元.试估计这批二手车一辆车获得利润的平均值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知空间几何体
 中,
中, 与
与 均为边长为2的等边三角形,
均为边长为2的等边三角形, 为腰长为3的等腰三角形,平面
为腰长为3的等腰三角形,平面 平面
平面 ,平面
,平面 平面
平面 分别为
分别为 的中点.
的中点.(1)求证:平面
 平面
平面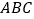 ;
;(2)求三棱锥
 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=bi(b∈R),
 是纯虚数,i是虚数单位.
是纯虚数,i是虚数单位.(1)求复数z;
(2)若复数(m+z)2所表示的点在第二象限,求实数m的取值范围.
相关试题

