【题目】如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.
(Ⅰ)若DC=2EF,求证:OE∥平面ADF;
(Ⅱ)求证:平面AFC⊥平面ABCD;
(Ⅲ)若AB=FB=2,AF=3,∠BCD=60°,求AF与平面ABCD所成角.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ) 30°.
【解析】试题分析: (Ⅰ)取AD的中点G,连接OG,FG,证明OGFE为平行四边形,可得OE∥FG,即可证明:OE∥平面ADF;
(Ⅱ)欲证:平面AFC⊥平面ABCD,即证BD⊥平面AFC;
(Ⅲ)做FH⊥AC于H,∠FAH为AF与平面ABCD所成角,即可求AF与平面ABCD所成角.
试题解析:
(Ⅰ)证明:取AD的中点G,连接OG,FG.
∵对角线AC与BD的交点为O,
∴OG∥DC,OG=![]() DC,
DC,
∵EF∥DC,DC=2EF,∴OG∥EF,OG=EF,∴OGFE为平行四边形,
∴OE∥FG,
∵FG平面ADF,OE平面ADF,
∴OE∥平面ADF;
(Ⅱ)证明:∵四边形ABCD为菱形,
∴OC⊥BD,
∵FD=FB,O是BD的中点,
∴OF⊥BD,
∵OF∩OC=O,
∴BD⊥平面AFC,
∵BD平面ABCD,
∴平面AFC⊥平面ABCD;
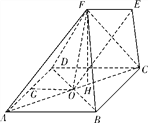
(Ⅲ)解:作FH⊥AC于H.
∵平面AFC⊥平面ABCD,∴FH⊥平面ABCD,
∴∠FAH为AF与平面ABCD所成角,
由题意,△BCD为正三角形,OA=![]() ,BD=AB=2,
,BD=AB=2,
∵FD=FB=2,
∴△FBD为正三角形,∴OF=![]() .
.
△AOF中,由余弦定理可得cos∠AOF=![]() =-
=-![]() ,
,
∴∠AOF=120°,
∴∠FAH=∠FAO=30°,
∴AF与平面ABCD所成角为30°

