(本小题满分14分) 如图,已知抛物线与坐标轴分别交于A 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D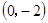 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线
.(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线 相切;(3)求线段MN的长(用
相切;(3)求线段MN的长(用 表示),并证明M、N两点到直线
表示),并证明M、N两点到直线 的距离之和等于线段MN的长.
的距离之和等于线段MN的长.

(1)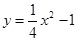 ;(2)见解析;
(3)
;(2)见解析;
(3)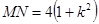
【解析】此题属于二次函数的综合题目,涉及了待定系数法求函数解析式、根与系数的关系,梯形的中位线定理,综合性较强,关键是要求同学们能将所学的知识融会贯通.
(1)设函数解析式为y=ax2+bx+c,然后利用待定系数法求解即可;
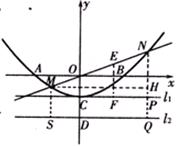
(2)设M(x1,y1),N(x2,y2),然后代入抛物线方程,用含y2的式子表示出ON,设ON的中点E,分别过点N、E向直线l、作垂线,垂足为P、F,利用梯形的中位线定理可得出EF,与所求ON的值进行比较即可得出结论;
(3)过点M作MH丄NP交NP于点H,在RT△MNH中表示出MN2,结合直线方程将MN2化简,求出MN,然后延长NP交l2于点Q,过点M作MS丄l2交l2于点S,则MS+NQ=y1+2+y2+2,利用根与系数的关系,求出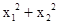 ,并代入,从而可得出结论。
,并代入,从而可得出结论。
解答:(1)设抛物线对应二次函数的解析式为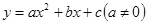
由
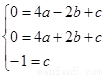 ,解得
,解得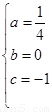 ,所以
,所以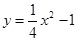 ……………………4分
……………………4分
(2)设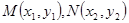 ,因为点M、N在抛物线上,
,因为点M、N在抛物线上,
所以 ,
,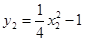 ,所以
,所以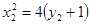 ;
;
又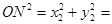
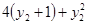 =
=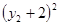 ,所以ON=
,所以ON=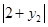 ,又因为
,又因为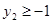 ,
,
所以ON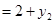
设ON的中点为E,分别过点N、E向直线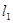 作垂线,垂足分别为P、F,
作垂线,垂足分别为P、F,
则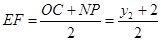 所以ON=2EF,
所以ON=2EF,
即ON的中点到直线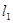 的距离等于ON长度的一半, 所以以ON为直径的圆与直线
的距离等于ON长度的一半, 所以以ON为直径的圆与直线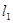 相切.
…………………………………9分
相切.
…………………………………9分
(3)过点M作MH⊥NP交NP于点H,则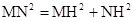
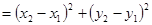
又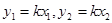 ,所以
,所以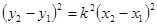
所以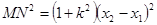 ;
;
又因为点M、N既在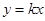 的图象上,又在抛物线上,所以
的图象上,又在抛物线上,所以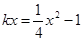 ,即
,即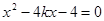 ,
,
所以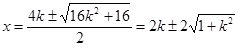 ,
,
所以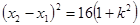 ,所以
,所以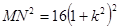 所以
所以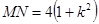
延长NP交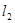 于点Q,过点M作MS⊥交
于点Q,过点M作MS⊥交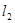 于点S,
于点S,
则MS+NQ=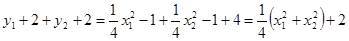
又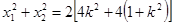 =
=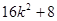 所以MS+NQ=
所以MS+NQ=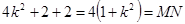
即MN两点到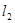 距离之和等于线段MN的长.…………………………………………14
距离之和等于线段MN的长.…………………………………………14

