【题目】从![]() 中这
中这![]() 个数中取
个数中取![]() 个数组成递增等差数列,所有可能的递增等差数列这个数记为
个数组成递增等差数列,所有可能的递增等差数列这个数记为![]() .
.
(1)当![]() 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及![]() 的值;
的值;
(2)求![]() ;
;
(3)求证:![]() .
.
参考答案:
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)通过列举,可知符合要求的递增等差数列为![]() 共
共![]() 个.所以
个.所以![]() ;(2)由于
;(2)由于![]() ,且
,且![]() ,即有
,即有![]() 项,所以
项,所以![]() ,故
,故![]() 取
取![]() ,
,![]() 取
取![]() 个,归纳出个数
个,归纳出个数![]() ;(3)由于
;(3)由于![]() ,按照(2)的方法,求出
,按照(2)的方法,求出![]() 的表达式,然后利用差比较法证明不等式.
的表达式,然后利用差比较法证明不等式.
试题解析:
(1) 符合要求的递增等差数列为![]() 共
共![]() 个.
个.![]() .
.
(2)设满足条件的一个等差数列首项为![]() ,公差为
,公差为![]() 的可能取值为
的可能取值为![]() .对于给定的
.对于给定的
![]() ,当
,当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个(如:
个(如: ![]() 时,
时,![]() ,当
,当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个:
个: ![]() ,其它同理)
,其它同理)![]() 当
当![]() 取
取![]() 时,可得符合要求的等差数列个数为:
时,可得符合要求的等差数列个数为:![]() .
.
(3)证明: 设等差数列首项为![]() ,公差为
,公差为![]() ,记
,记![]() 的整数部分是
的整数部分是![]() ,则
,则![]() ,即
,即![]() .
.![]() 的可能取值为
的可能取值为![]() ,对于给定的
,对于给定的![]() , 当
, 当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个.
个.![]() 当
当![]() 取
取![]() 时,符合要求的等差数列个数
时,符合要求的等差数列个数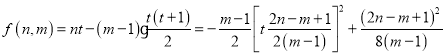 .由题意
.由题意![]() .又
.又 ,
,
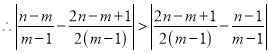 .
.
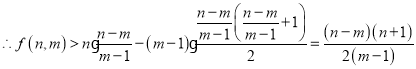 . 即
. 即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
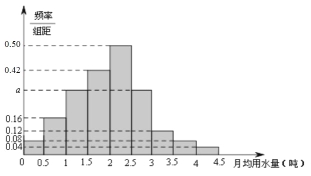
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
 ,底面
,底面 为菱形,
为菱形,  平面
平面 ,
,  ,
,  分别是
分别是 的中点.
的中点.(Ⅰ)证明:
 ;
;(Ⅱ)若
 为
为 上的动点,
上的动点,  与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
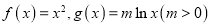 ,已知
,已知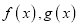 在
在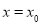 处的切线
处的切线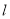 相同.
相同.(1)求
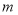 的值及切线
的值及切线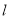 的方程;
的方程;(2)设函数
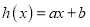 ,若存在实数
,若存在实数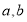 使得关于
使得关于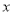 的不等式
的不等式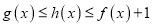 对
对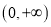 上的任意实数
上的任意实数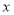 恒成立,求
恒成立,求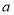 的最小值及对应的
的最小值及对应的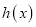 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的顶点C在直线3x﹣y=0上,顶点A、B的坐标分别为(4,2),(0,5).
(Ⅰ)求过点A且在x,y轴上的截距相等的直线方程;
(Ⅱ)若△ABC的面积为10,求顶点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台举行一个比赛类型的娱乐节目,
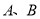 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将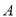 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家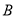 队的平均分比
队的平均分比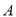 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.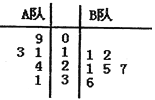
(1)根据茎叶图中的数据,求出
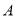 队第六位选手的成绩;
队第六位选手的成绩;(2)主持人从
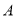 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;(3)主持人从
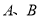 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为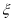 ,求
,求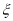 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆x2+y2-6x-8y+21=0和直线kx-y-4k+3=0.
(1)若直线和圆总有两个不同的公共点,求k的取值集合
(2)求当k取何值时,直线被圆截得的弦最短,并求这最短弦的长.
相关试题

