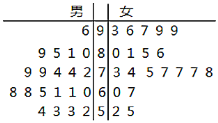
【题目】为了响应国家号召，促进垃圾分类，某校组织了高三年级学生参与了“垃圾分类，从我做起”的知识问卷作答，随机抽出男女各20名同学的问卷进行打分，作出如图所示的茎叶图，成绩大于70分的为“合格”.

男

女

总计

合格

不合格

总计

（1）由以上数据绘制成2×2联表，是否有95%以上的把握认为“性别”与“问卷结果”有关？

（2）从上述样本中，成绩在60分以下（不含60分）的男女学生问卷中任意选2个，求这2个学生性别不同的概率.

附：

0.100

0.050

0.010

0.001

2.706

3.841

6.635

10.828

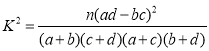
【答案】（1）列联表见解析，有；（2）.

【解析】

（1）根据题意填写列联表，计算即可作出判断；

（2）利用列举法以及古典概型概率公式计算即可.

（1）根据茎叶图可得

男

女

总计

合格

10

16

26

不合格

10

4

14

总计

20

20

40

知有95%以上的把握认为“性别”与“问卷结果”有关.

（2）从茎叶图可知，成绩在60分以下（不含60分）的男女学生人数分别是4人和2人，分别用，，，和，表示

基本事件为：，，，，，，，，，，，，，，共有15个

其中性别不同的基本事件有，，，，，，，共8个

所求概率为.

关闭