已知等差数列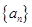 的公差
的公差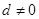 ,它的前
,它的前 项和为
项和为 ,若
,若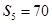 ,且
,且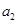 、
、 、
、 成等比数列.
成等比数列.
(1)求数列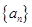 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,求证:
,求证: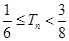 .
.
(1)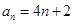 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)先利用基本量法列二元一次方程组求出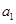 和
和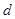 ,然后利用等差数列的通项公式求出数列
,然后利用等差数列的通项公式求出数列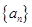 的通项公式;(2)先利用等差数列的求和公式求出
的通项公式;(2)先利用等差数列的求和公式求出 ,并利用裂项求和法求出数列
,并利用裂项求和法求出数列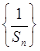 的前
的前 项和
项和 ,从而证明
,从而证明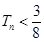 ,再利用作差法得出数列
,再利用作差法得出数列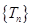 的单调性,从而得出数列
的单调性,从而得出数列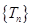 中的最小项为
中的最小项为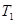 ,从而证明
,从而证明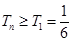 ,进而证明所得不等式.
,进而证明所得不等式.
试题解析:(1)由题意知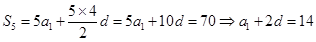 ,
,
且 ,整理得
,整理得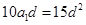 ,由于
,由于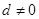 ,
,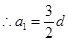 ,
,
于是有 ,
,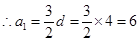 ,
,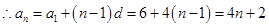 ;
;
(2)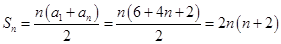 ,
, ,
,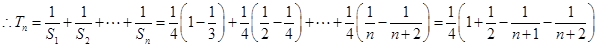
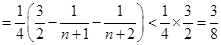 ,
,
由于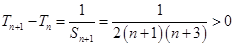 ,所以数列
,所以数列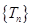 单调递增,故
单调递增,故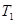 最小,
最小,
即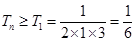 ,综上所述
,综上所述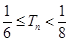 .
.
考点:1.等差数列的通项公式;2.等差数列求和;3.裂项求和法

