搜索
【题目】已知点F1 ， F2分别是双曲线 
的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A，B两点，若△ABF2是锐角三角形，则该双曲线离心率的取值范围是（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】解：在双曲线 
中，
令x=﹣c 得，y=± 
，∴A，B两点的纵坐标分别为± ．
由△ABF2是锐角三角形知，∠AF2F1＜ 
，tan∠AF2F1= 
＜tan =1，
∴ 
＜1，c2﹣2ac﹣a2＜0，e2﹣2e﹣1＜0，∴1﹣ 
＜e＜1+ ．
又 e＞1，∴1＜e＜1+ ，
故选D．
先求出A，B两点的纵坐标，由△ABF2是锐角三角形知，tan∠AF2F1= ＜1，e2﹣2e﹣1＜0，解不等式求出e 的范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，经过村庄A有两条互相垂直的笔直公路AB和AC，根据规划拟在两条公路围成的直角区域内建一工厂P，为了仓库存储和运输方便，在两条公路上分别建两个仓库M，N（异于村庄A，将工厂P及仓库M，N近似看成点，且M，N分别在射线AB，AC上），要求MN=2，PN=1（单位：km），PN⊥MN．
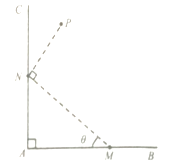
（1）设∠AMN=θ，将工厂与村庄的距离PA表示为θ的函数，记为l（θ），并写出函数l（θ）的定义域；
（2）当θ为何值时，l（θ）有最大值？并求出该最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=m（sinx+cosx）﹣4sinxcosx，x∈[0，
]，m∈R．
（1）设t=sinx+cosx，x∈[0， ]，将f（x）表示为关于t的函数关系式g（t），并求出t的取值范围；
（2）若关于x的不等式f（x）≥0对所有的x∈[0， ]恒成立，求实数m的取值范围；
（3）若关于x的方程f（x）﹣2m+4=0在[0， ]上有实数根，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C的中心在原点，焦点在x轴上，离心率等于
，它的一个短轴端点是（0，2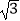 
）． 
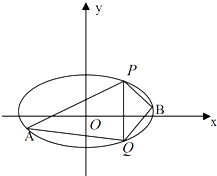
（1）求椭圆C的方程；
（2）P（2，3）、Q（2，﹣3）是椭圆上两点，A、B是椭圆位于直线PQ两侧的两动点，
①若直线AB的斜率为 ，求四边形APBQ面积的最大值；
②当A、B运动时，满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值，请说明理由． -
科目： 来源： 题型：
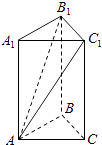
查看答案和解析>>【题目】如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，底面是边长为2的正三角形，侧棱长为3，则BB1与平面AB1C1所成的角是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题
（1）已知函数f（x）=2x+
（x＞0），证明函数f（x）在（0， 
）上单调递减，并写出函数f（x）的单调递增区间；
（2）记函数g（x）=a|x|+2ax（a＞1） ①若a=4，解关于x的方程g（x）=3；
②若x∈[﹣1，+∞），求函数g（x）的值域． -
科目： 来源： 题型：
查看答案和解析>>【题目】设f（x）是定义在R上的函数，f（0）=2，对任意x∈R，f（x）+f′（x）＞1，则不等式exf（x）＞ex+1的解集为（ ）
A.（0，+∞）
B.（﹣∞，0）
C.（﹣∞，﹣1）∪（1，+∞）
D.（﹣∞，﹣1）∪（0，1）
相关试题
