【题目】已知函数f(x)= ![]() ( e为自然对数的底数),且f(3a﹣2)>f(a﹣1),则实数a的取值范围为_____.
( e为自然对数的底数),且f(3a﹣2)>f(a﹣1),则实数a的取值范围为_____.
参考答案:
【答案】(﹣∞,![]() )∪(
)∪(![]() ,+∞)
,+∞)
【解析】
根据函数式子得出f(﹣x)=f(x)=f(|x|),且在(0,+∞)单调递增,把f(3a﹣2)>f(a﹣1),转化为|3a﹣2|>|a﹣1|,即8a2﹣10a+3>0,求解即得到实数a的取值范围.
∵函数f(x)=e|x|+x2(e为自然对数的底数)为偶函数,
∴f(﹣x)=f(x)=f(|x|),且在(0,+∞)单调递增,
∵f(3a﹣2)>f(a﹣1),
∴|3a﹣2|>|a﹣1|,
即8a2﹣10a+3>0,
实数a的取值范围为a![]() 或a
或a![]() ,
,
故答案为:(﹣∞,![]() )∪(
)∪(![]() ,+∞)
,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
组号
分组
回答正确的人数
回答正确的人数
占本组的频率第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
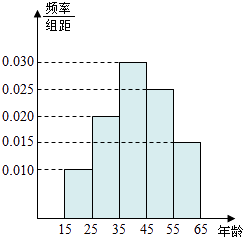
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)判断函数
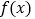 在
在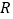 的单调性.(不需要证明);
的单调性.(不需要证明);(2)探究是否存在实数
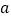 ,使得函数
,使得函数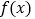 为奇函数?若存在,求出
为奇函数?若存在,求出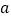 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)在(2)的条件下,解不等式
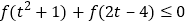 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, .
.(1)直接写出函数
 的增区间(不需要证明);
的增区间(不需要证明);(2)求出函数
 ,
, 的解析式;
的解析式;(3)若函数
 ,
, ,求函数
,求函数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
 .
.(1)若
 ,求
,求 的概率;
的概率;(2)若
 ,求
,求 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥A﹣BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
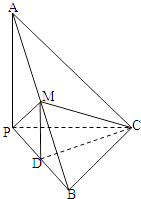
(1)求证:BC⊥平面APC;
(2)若BC=3,AB=10,求三棱锥B﹣MDC的体积VB﹣MDC . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,记不等式f(x)≤4的解集为M,记函数
,记不等式f(x)≤4的解集为M,记函数 的定义域为集合N.
的定义域为集合N.(Ⅰ)求集合M和N;
(Ⅱ)求M∩N和M∪(RN).
相关试题

