【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,对于任意正实数
时,对于任意正实数![]() ,不等式
,不等式![]() 恒成立,试判断实数
恒成立,试判断实数![]() 的大小关系.
的大小关系.
参考答案:
【答案】(1)当![]() 时
时![]() 增;
增;![]() 减;当
减;当![]() 时
时![]() 减;
减;![]() 增;(2)
增;(2)![]()
【解析】
(1)求出函数的导数,分类讨论,即可求解函数的单调性;
(2)设![]() ,求导数判断函数的单调性,求出函数的极值,转化为
,求导数判断函数的单调性,求出函数的极值,转化为![]() ,即可求解.
,即可求解.
(1)由题意,函数![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,在
时,在![]() 上,
上,![]() ,函数
,函数![]() 单调递增;
单调递增;
在![]() 上,
上,![]() ,函数
,函数![]() 单调递减.
单调递减.
当![]() 时,在
时,在![]() 上,
上,![]() ,函数
,函数![]() 单调递减;
单调递减;
在![]() 上,
上,![]() ,函数
,函数![]() 单调递增.
单调递增.
综上可得:当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;当
单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)当![]() 时,设
时,设![]()
则![]() ,令
,令![]() ,即
,即![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,即
,即![]() 单调递减,
单调递减,
所以![]() ,
,
要使得不等式![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,
,
所以![]() ,故实数
,故实数![]() 的大小关系为
的大小关系为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,海中一小岛C周围
 nmile内有暗礁,货轮由西向东航行至A处测得小岛C位于北偏东75°方向上,航行8nmile后,于B处测得小岛C在北偏东60°方向上.
nmile内有暗礁,货轮由西向东航行至A处测得小岛C位于北偏东75°方向上,航行8nmile后,于B处测得小岛C在北偏东60°方向上.
(1)如果这艘货轮不改变航向继续前进,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘货轮在B处改变航向为南偏东α°(α>0)方向航行,顺利绕过暗礁,求a的最大值.(附:
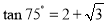 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
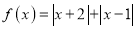 .
.(Ⅰ)求
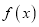 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
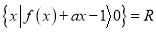 ,求实数
,求实数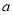 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
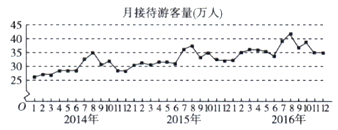
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的最大值为
的最大值为 .
.(1)若关于
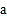 的方程
的方程 的两个实数根为
的两个实数根为 ,求证:
,求证: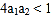 ;
;(2)当
 时,证明函数
时,证明函数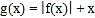 在函数
在函数 的最小零点
的最小零点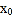 处取得极小值.
处取得极小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
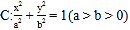 的一个焦点为
的一个焦点为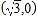 ,离心率为
,离心率为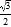 .不过原点的直线
.不过原点的直线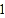 与椭圆
与椭圆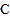 相交于
相交于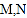 两点,设直线
两点,设直线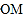 ,直线
,直线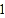 ,直线
,直线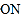 的斜率分别为
的斜率分别为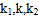 ,且
,且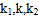 成等比数列.
成等比数列.(1)求
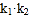 的值;
的值;(2)若点
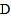 在椭圆
在椭圆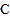 上,满足
上,满足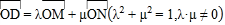 的直线
的直线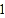 是否存在?若存在,求出直线
是否存在?若存在,求出直线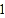 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
相关试题

