【题目】如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴长为( ) 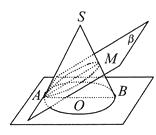
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解答:过椭圆C作平行于圆锥底面的截面(圆形),交AS,BS于R,T,交椭圆C于两点P,Q,则P,Q即是椭圆短半轴顶点,在所作的圆中,RT为直径,如图, 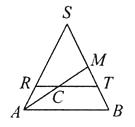
因为轴截面△SAB是边长为4的正三角形,C为AM的中点,所以TC= ![]() AB=2,RC=
AB=2,RC= ![]() AB=1,,因为PQ⊥RT,所以PC=CQ,所以利用相交弦定理可得:PC·CQ=TC·RC,所以PC=
AB=1,,因为PQ⊥RT,所以PC=CQ,所以利用相交弦定理可得:PC·CQ=TC·RC,所以PC= ![]() .所以橄圆C的短半轴为
.所以橄圆C的短半轴为 ![]() .
.
分析:本题主要考查了平面与圆锥面的截线,解决问题的关键是根据平面与圆锥面的截线的性质结合所给几何关系利用相交弦的性质分析计算即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B.
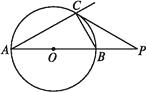
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的个数是( )
①向量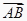 与
与 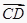 是共线向量,则A、B、C、D必在同一直线上;
是共线向量,则A、B、C、D必在同一直线上;
②向量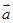 与向量
与向量 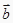 平行,则
平行,则 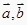 方向相同或相反;
方向相同或相反;
③若下列向量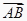 、
、 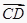 满足
满足 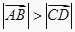 ,且
,且 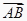 与
与 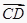 同向,则
同向,则  ;
;
④若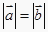 ,则
,则 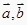 的长度相等且方向相同或相反;
的长度相等且方向相同或相反;
⑤由于零向量方向不确定,故不能与任何向量平行.
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】【选修4—4:坐标系与参数方程】
将圆
 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.(Ⅰ)写出C的参数方程;
(Ⅱ)设直线
 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段 的中点且与
的中点且与 垂直的直线的极坐标方程.
垂直的直线的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的奇函数,当x>0时,f(x)=x2+2x﹣1
(1)求f(﹣3)的值;
(2)求函数f(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】轴截面是边长为4
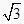 的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 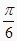 ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( ) 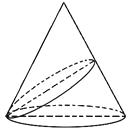
A.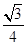
B.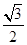
C.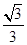
D.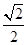
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是①
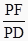 ; ②
; ② 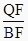 ; ③
; ③ 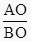 ; ④
; ④ 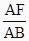 ; ⑤
; ⑤  其中正确的是( )
其中正确的是( )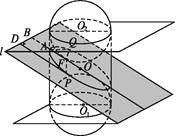
A.①②
B.①③④
C.②③⑤
D.①②③④⑤
相关试题

