【题目】如图,四边形ABCD、ADEF为正方形,G,H是DF,FC的中点. 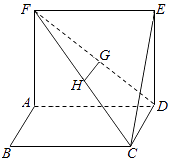
(1)求证:GH∥平面CDE;
(2)求证:BC⊥平面CDE.
参考答案:
【答案】
(1)证明:∵G,H是DF,FC的中点.
∴GH∥CD,
又GH平面CDE,CD平面CDE,
∴GH∥平面CDE
(2)证明:∵四边形ABCD、ADEF为正方形,
∴DE⊥AD,CD⊥AD,BC∥AD.
又DE平面CDE,CD平面CDE,CD∩DE=D,
∴AD⊥平面CDE,
又BC∥AD,
∴BC⊥平面CDE
【解析】(1)由中位线定理得出GH∥CD,故GH∥平面CDE;(2)由AD⊥CD,AD⊥DE得出AD⊥平面CDE,而BC∥AD,故BC⊥平面CDE.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求经过三点A(1,4),B(﹣2,3),C(4,﹣5)的圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4 坐标系与参数方程
在直角坐标系
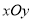 中,圆
中,圆 ,曲线
,曲线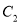 的参数方程为
的参数方程为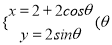 为参数),并以
为参数),并以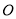 为极点,
为极点, 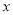 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)写出
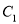 的极坐标方程,并将
的极坐标方程,并将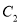 化为普通方程;
化为普通方程;(2)若直线
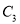 的极坐标方程为
的极坐标方程为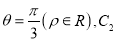 与
与 相交于
相交于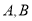 两点,
两点,求
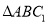 的面积(
的面积(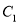 为圆
为圆 的圆心).
的圆心). -
科目: 来源: 题型:
查看答案和解析>>【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同轨班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的
 列联表(单位:人)
列联表(单位:人)
(1)能够据此判断有97.5%把握热内加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在5—7分钟,小刚正确解得一道数学应用题所用的时间在6—8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明现正确解答完的概率;
(3)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们点答题情况进行全程研究,记A、B两人中被抽到的人数为X,求X的分布列及数学期望E(X).

-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
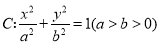 过点
过点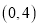 ,离心率为
,离心率为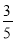 .
.(1)求椭圆
 的方程;
的方程;(2)求过点
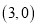 且斜率为
且斜率为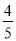 的直线被椭圆
的直线被椭圆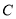 所截线段的中点坐标.
所截线段的中点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
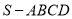 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的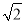 倍,P为侧棱SD上的点,且
倍,P为侧棱SD上的点,且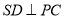 .
.(1)求二面角
 的大小;
的大小;(2)在侧棱SC上是否存在一点E,使得
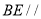 平面
平面 ?若存在,求
?若存在,求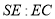 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.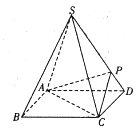
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
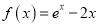 .
.(1)求函数
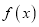 的极值;
的极值;(2)当
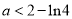 且
且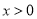 时,试比较
时,试比较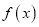 与
与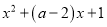 的大小.
的大小.
相关试题

