Question

【题目】3月底，我国新冠肺炎疫情得到有效防控，但海外确诊病例却持续暴增，防疫物资供不应求，某医疗器械厂开足马力，日夜生产防疫所需物品.已知该厂有两条不同生产线和生产同一种产品各10万件，为保证质量，现从各自生产的产品中分别随机抽取20件，进行品质鉴定，鉴定成绩的茎叶图如下所示：

该产品的质量评价标准规定：鉴定成绩达到的产品，质量等级为优秀；鉴定成绩达到的产品，质量等级为良好；鉴定成绩达到的产品，质量等级为合格.

（1）从等级为优秀的样本中随机抽取两件，求两件均由生产线生产的概率；

（2）请完成下面质量等级与生产线产品列联表，并判断能不能在误差不超过0.05的情况下，认为产品等级是否达到良好以上与生产产品的生产线有关.

	生产线的产品	生产线的产品	合计
良好以上
合格
合计

附：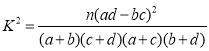

	0.10	0.05	0.01	0.005
	2.706	3.841	6.635	7.879

Answer 1

【答案】（1）（2）见解析，不能

【解析】

（1）利用古典概型的概率公式求两件均由生产线生产的概率；（2）先完成质量等级与生产线产品列联表，再利用独立性检验计算判断得解.

（1）从茎叶图知，样本中优秀的产品有2件来自生产线，3件来自生产线；

设生产线的产品为，，生产线的产品分别为，

从这5件优秀产品中任意抽取两件的所有情况有：

，，，，，，，，，共10种，

其中均来自生产线的有，，共3种，

两件均由生产线生产的概率为.

（2）由已知可得，列联表为

	生产线的产品	生产线的产品	合计
良好以上	6	12	18
合格	14	8	22
合计	20	20	40

，

所以不能在误差不超过0.05的情况下，认为产品等级是否达到良好以上与生产产品的生产线有关.