【题目】已知双曲线![]() 的两条渐近线与抛物线
的两条渐近线与抛物线![]() 的准线分别交于A,B两点,O为坐标原点,若
的准线分别交于A,B两点,O为坐标原点,若![]() ,则双曲线的离心率
,则双曲线的离心率![]() __________.
__________.
【答案】![]()
【解析】因为双曲线![]() 的两条渐近线为
的两条渐近线为![]() ,抛物线
,抛物线![]() 的准线为
的准线为![]() ,所以
,所以![]() ,
,
因此![]()
点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于![]() 的方程或不等式,再根据
的方程或不等式,再根据![]() 的关系消掉
的关系消掉![]() 得到
得到![]() 的关系式,而建立关于
的关系式,而建立关于![]() 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
【题型】填空题
【结束】
16
【题目】若函数![]() 满足:对于
满足:对于![]() 图象上任意一点P,在其图象上总存在点
图象上任意一点P,在其图象上总存在点![]() ,使得
,使得![]() 成立,称函数
成立,称函数![]() 是“特殊对点函数”.给出下列五个函数:
是“特殊对点函数”.给出下列五个函数:
①![]() ;②
;②![]() (其中e为自然对数的底数);③
(其中e为自然对数的底数);③![]() ;④
;④![]() ;
;
⑤![]() .
.
其中是“特殊对点函数”的序号是__________.(写出所有正确的序号)
【答案】②④⑤
【解析】设![]() 由
由![]() 得
得![]() , 或
, 或![]() ;
;
①![]() ,所以不是“特殊对点函数”;
,所以不是“特殊对点函数”;
②由图知,对于任意一点P,在其图象上总存在点![]() ,使得
,使得![]() ,所以是“特殊对点函数”;
,所以是“特殊对点函数”;
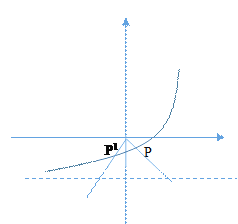
③对于![]()
![]() ;所以不是“特殊对点函数”;
;所以不是“特殊对点函数”;
④由图知,对于任意一点P,在其图象上总存在点![]() ,使得
,使得![]() ,所以是“特殊对点函数”;
,所以是“特殊对点函数”;
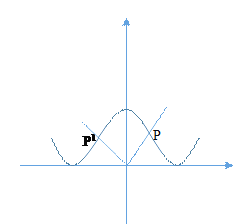
⑤由图知,对于任意一点P,在其图象上总存在点![]() ,使得
,使得![]() ,所以是“特殊对点函数”;
,所以是“特殊对点函数”;
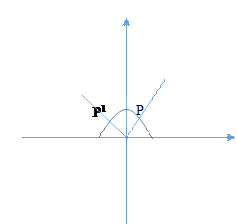
综上“特殊对点函数”的序号是②④⑤

