下列四个命题中的真命题为
- A.若sinA=sinB,则∠A=∠B
- B.若lgx2=0,则x=1
- C.任意x∈R,都有x2+1>0
- D.存在x∈Z,使1<4x<3
C
分析:若sinA=sinB,则∠A=2kπ+∠B或∠A=2kπ+π-∠B,判断出A错;若lgx2=0,则x2=1则x=±1,判断出B错;任意x∈R,都有x2+1>0,判断出C对;因为1<4x<3得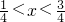 ,所以不存在x∈Z使1<4x<3,判断出D错.
,所以不存在x∈Z使1<4x<3,判断出D错.
解答:对于A,若sinA=sinB,则∠A=2kπ+∠B或∠A=2kπ+π-∠B,故A错;
对于B,若lgx2=0,则x2=1则x=±1,故B错;
对于C,任意x∈R,都有x2+1>0,故C对;
对于D1<4x<3得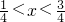 ,所以不存在x∈Z使1<4x<3
,所以不存在x∈Z使1<4x<3
故选C.
点评:判断全称命题为真需证得对于所有的元素都满足属性,判断其为假,只需举一个反例即可;当特称全称命题为假需证得对于所有的元素都不满足属性,判断其为真,只需举一个反例即可.
分析:若sinA=sinB,则∠A=2kπ+∠B或∠A=2kπ+π-∠B,判断出A错;若lgx2=0,则x2=1则x=±1,判断出B错;任意x∈R,都有x2+1>0,判断出C对;因为1<4x<3得
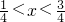 ,所以不存在x∈Z使1<4x<3,判断出D错.
,所以不存在x∈Z使1<4x<3,判断出D错.解答:对于A,若sinA=sinB,则∠A=2kπ+∠B或∠A=2kπ+π-∠B,故A错;
对于B,若lgx2=0,则x2=1则x=±1,故B错;
对于C,任意x∈R,都有x2+1>0,故C对;
对于D1<4x<3得
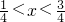 ,所以不存在x∈Z使1<4x<3
,所以不存在x∈Z使1<4x<3故选C.
点评:判断全称命题为真需证得对于所有的元素都满足属性,判断其为假,只需举一个反例即可;当特称全称命题为假需证得对于所有的元素都不满足属性,判断其为真,只需举一个反例即可.

