【题目】已知抛物线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() ,
,![]() 分别作
分别作![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() .
.
(1)记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明:
,证明:![]()
![]() 为定值;
为定值;
(2)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() ,
,![]() 的坐标分别为
的坐标分别为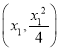 ,
,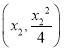 ,利用导数的几何意义知
,利用导数的几何意义知![]() ,
,![]() ,联立直线与抛物线的方程结合韦达定理可得结果;
,联立直线与抛物线的方程结合韦达定理可得结果;
(2)首先得出切线![]() ,
,![]() 的方程,求出
的方程,求出![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() ,由三角形面积公式结合二次函数的性质得结果.
,由三角形面积公式结合二次函数的性质得结果.
(1)证明:因为![]() ,
,![]() 两点在曲线
两点在曲线![]() 上,故设
上,故设![]() ,
,![]() 的坐标分别为
的坐标分别为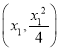 ,
,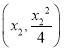 .
.
因为![]() ,所以
,所以![]() ,则
,则![]() ,
,![]() .
.
设直线![]() 的斜率为
的斜率为![]() ,则其方程为
,则其方程为![]() ,由
,由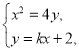 得
得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() 为定值.
为定值.
(2)解:设![]() 点坐标为
点坐标为![]() ,
,
由(1)知切线![]() 的方程为
的方程为![]() ①
①
切线![]() 的方程为
的方程为![]() ②,
②,
①![]() ②得
②得![]() ;
;
①![]() ②
②![]() 得
得![]() .
.
由(1)知![]() ,
,![]() ,所以
,所以![]() 点坐标为
点坐标为![]() ,
,
所以![]()
![]() .
.
因为点![]() 到直线
到直线![]() 的距离
的距离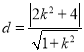 .
.
所以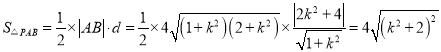 .
.
因为![]() ,所以当
,所以当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.

