【题目】若函数f(x)=lnx+ax2﹣(a+2)x在 ![]() 处取得极大值,则正数a的取值范围是
处取得极大值,则正数a的取值范围是
参考答案:
【答案】(0,2)
【解析】解:f(x)的定义域是(0,+∞),
f′(x)= ![]() +2ax﹣(a+2)=
+2ax﹣(a+2)= ![]() ,
,
①a≤0时,ax﹣1<0,
令f′(x)>0,解得:x> ![]() ,令f′(x)<0,解得:0<x<
,令f′(x)<0,解得:0<x< ![]() ,
,
故 ![]() 是函数的极小值点,不合题意,
是函数的极小值点,不合题意,
②0<a<2时, ![]() <
< ![]() ,
,
令f′(x)>0,解得:x< ![]() 或x>
或x> ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴函数f(x)在 ![]() 处取得极大值,符合题意,
处取得极大值,符合题意,
③a=2时,f′(x)≥0,f(x)递增,无极值,
④a>2时, ![]() >
> ![]() ,
,
令f′(x)>0,解得:x> ![]() 或x<
或x< ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴函数f(x)在x= ![]() 处取得极大值,不符合题意,
处取得极大值,不符合题意,
综上,a∈(0,2),
所以答案是:(0,2).
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是
 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数ξ的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
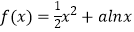 .
.
(1)当a<0时,若x>0,使f(x)≤0成立,求a的取值范围;
(2)令g(x)=f(x)﹣(a+1)x,a∈(1,e],证明:对x1 , x2∈[1,a],恒有|g(x1)﹣g(x2)|<1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为
 ,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
(1)求椭圆E的方程;
(2)求l1的斜率k的取值范围;
(3)求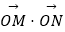 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设Sn是等比数列{an}的前n项和,S3 , S9 , S6成等差数列,且a2+a5=2am , 则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项Sn=(﹣1)n
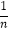 ,若存在正整数n,使得(an﹣1﹣p)(an﹣p)<0成立,则实数p的取值范围是 .
,若存在正整数n,使得(an﹣1﹣p)(an﹣p)<0成立,则实数p的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|ex﹣e2a|,若f(x)在区间(﹣1,3﹣a)内的图象上存在两点,在这两点处的切线相互垂直,则实数a的取值范围是 .
相关试题

