直线kx-y+1=3k,当k变动时,所有直线都通过定点
- A.(0,0)
- B.(0,1)
- C.(3,1)
- D.(2,1)
C
分析:将直线的方程变形为k(x-3)=y-1 对于任何k∈R都成立,从而有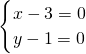 ,解出定点的坐标.
,解出定点的坐标.
解答:由kx-y+1=3k得k(x-3)=y-1
对于任何k∈R都成立,则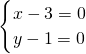 ,
,
解得 x=3,y=1,
故直线经过定点(3,1),故选 C.
点评:本题考查直线过定点问题,把直线方程变形为参数乘以一个因式再加上另一个因式等于0的形式恒成立,故这两个因式都等于0.
分析:将直线的方程变形为k(x-3)=y-1 对于任何k∈R都成立,从而有
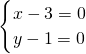 ,解出定点的坐标.
,解出定点的坐标.解答:由kx-y+1=3k得k(x-3)=y-1
对于任何k∈R都成立,则
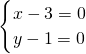 ,
,解得 x=3,y=1,
故直线经过定点(3,1),故选 C.
点评:本题考查直线过定点问题,把直线方程变形为参数乘以一个因式再加上另一个因式等于0的形式恒成立,故这两个因式都等于0.

