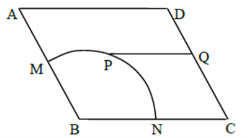
【题目】如图，某广场中间有一块边长为2百米的菱形状绿化区，其中是半径为1百米的扇形，． 管理部门欲在该地从到修建小路：在弧上选一点（异于两点），过点修建与平行的小路．问：点选择在何处时，才能使得修建的小路与及的总长最小？并说明理由．

【答案】时,总长最小.

【解析】

试题分析：由题意,,过分别作的垂线,在直角三角形中用表示线段长度,将总长最小转化为三角函数的最值问题,对函数求导判断单调性,得出在时,总长最小.

试题解析：解：连接，过作垂足为，过作垂足为，

设，

若，在中，，

若，则，

若，则，

∴．．．．．．．．．．．．．．．．．．．．．4分

在中，,

………………………………6分

所以总路径长，．．．．．．．．．．．．．8分

．．．．．．．．．．．．．．．．．．．．．．．10分

令，当时，，

当时，．．．．．．．．．．．．．．．．．．．．．．．．．．．．11分

所以当时，总路径最短．

答：当时，总路径最短．．．．．．．．．．．．．．．．．．．．．．．12分

关闭