【题目】已知函数![]() ,以下关于
,以下关于![]() 的结论其中正确的结论是( )
的结论其中正确的结论是( )
①当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
②当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
③当![]() 时,
时,![]() 在
在![]() 上有无数个极值点;
上有无数个极值点;
④当![]() 时,
时,![]() 在
在![]() 上恒成立.
上恒成立.
A.①④B.②③C.①②④D.②③④
【答案】D
【解析】
根据零点存在性定理,可判断①;通过求导,判断![]() 符号以及零点的个数,可判断②③;利用导数结合不等式性质可判断④,即可得出结论.
符号以及零点的个数,可判断②③;利用导数结合不等式性质可判断④,即可得出结论.
对于①:当![]() 时,
时,![]()
![]() ,
,
![]() ,
,
![]() 在
在![]() 存在零点,所以①错误;
存在零点,所以①错误;
对于②:当![]() 时,
时,![]()
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() ,
,
当![]() ,
,![]() 恒成立,
恒成立,
故![]() 在
在![]() 上单调递增,故②正确
上单调递增,故②正确
对于③:当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ,
,
画出![]() 和
和![]() 作出如图,
作出如图,
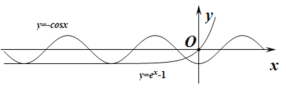
当![]() 时,
时,![]() ,
,
![]() 和
和![]() 在
在![]() 有无数个交点,
有无数个交点,
交点的横坐标为![]() 的极值点,
的极值点,
故此时,![]() 在
在![]() 上有无数个极值点;故③正确
上有无数个极值点;故③正确
对于④:当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
令![]() ,得
,得![]() ,
,
所以![]() 单调递减,故当
单调递减,故当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,进一步分析,
,进一步分析,
当![]() 时,
时,![]() ,
,
对于![]() ,得
,得![]() ,
,![]() 单调递增,
单调递增,
且![]() 单调递减,
单调递减,
![]() 单调递增,
单调递增,
![]() 时,
时,![]() 取得极小值,也是最小为
取得极小值,也是最小为![]() ,
,
![]() ,
,
![]() 在
在![]() 上恒大于0,即
上恒大于0,即![]() ,
,
当![]() ,
,![]()
![]() ,在
,在![]() 时有
时有![]() ,故
,故![]() 单调递增,
单调递增,
且![]() ,所以
,所以![]() ,
,
所以,![]()
综上,当![]() 时,
时,![]() 在
在![]() 上恒成立,故④正确
上恒成立,故④正确
故答案为:D

