【题目】如图，已知双曲线C： ﹣y2=1（a＞0）的右焦点为F，点A，B分别在C的两条渐近线AF⊥x轴，AB⊥OB，BF∥OA（O为坐标原点）．

（1）求双曲线C的方程；
（2）过C上一点P（x0 ， y0）（y0≠0）的直线l： ﹣y0y=1与直线AF相交于点M，与直线x= 相交于点N．证明：当点P在C上移动时， 恒为定值，并求此定值．

【答案】
（1）解：依题意知，A（c， ），设B（t，﹣ ），

∵AB⊥OB，BF∥OA，∴ =﹣1， = ，

整理得：t= ，a= ，

∴双曲线C的方程为 ﹣y2=1


（2）证明：由（1）知A（2， ），l的方程为： ﹣y0y=1，

又F（2，0），直线l： ﹣y0y=1与直线AF相交于点M，与直线x= 相交于点N．

于是可得M（2， ），N（ ， ），

∴ = = = = =


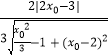【解析】（1）依题意知，A（c， ），设B（t，﹣ ），利用AB⊥OB，BF∥OA，可求得a= ，从而可得双曲线C的方程；（2）易求A（2， ），l的方程为： ﹣y0y=1，直线l： ﹣y0y=1与直线AF相交于点M，与直线x= 相交于点N，可求得M（2， ），N（ ， ），于是化简 = 可得其值为 ，于是原结论得证．

关闭