【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]() BC=1,E是PC的中点,平面PAC⊥平面ABCD.
BC=1,E是PC的中点,平面PAC⊥平面ABCD.

(1)证明:ED∥平面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
参考答案:
【答案】
【解析】(1)如图,取PB的中点F,连接AF,![]() .
.
∵EF是![]() 的中位线,∴EF∥BC,且EF=
的中位线,∴EF∥BC,且EF=![]() .(2分)
.(2分)
又![]() ,且AD=
,且AD=![]() ,∴AD∥EF且AD=EF,则四边形ADEF是平行四边形.
,∴AD∥EF且AD=EF,则四边形ADEF是平行四边形.
∴DE∥AF,又DE平面ABP,AF平面ABP,∴ED∥平面PAB.(5分)
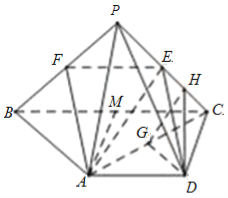
(2)如图,取BC的中点M,连接AM,则AD∥MC且AD=MC,∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上,∴AB⊥AC,可得![]() .
.
过D作DG⊥AC于G,∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴DG⊥平面PAC,则DG⊥PC.
过G作![]() 于
于![]() ,则PC⊥平面GHD,连接DH,则PC⊥DH,
,则PC⊥平面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.(9分)
在![]() 中,
中,![]() ,连接AE,
,连接AE,![]() .
.
在![]() 中,
中,![]() ,则
,则![]() .
.
即二面角A﹣PC﹣D的余弦值为![]() .(12分)
.(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
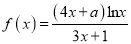 ,曲线
,曲线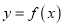 在点
在点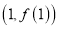 处的切线与直线
处的切线与直线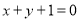 垂直.
垂直.(1)求
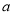 的值;
的值;(2)若对于任意的
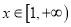 ,
, 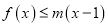 恒成立,求
恒成立,求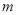 的取值范围;
的取值范围;(3)求证:
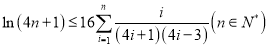 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的
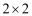 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为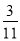 .
.优秀
非优秀
合计
甲班
10
乙班
30
合计
110
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
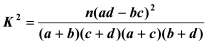 。
。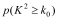
0.100
0.050
0.025
0.010
0.001
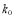
2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=(m2-5m+1)xm+1为幂函数,且为奇函数.
(I)求m的值;
(II)求函数g(x)=h(x)+
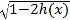 ,x∈
,x∈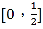 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上的点,且AM=BN,将三角形ADE沿AE折起,则下列说法正确的是 (填上所有正确说法的序号).
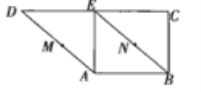
①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;
②不论D折至何位置都有MN⊥AE;
③不论D折至何位置(不在平面ABC内)都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x+1,x∈N*.若x0,n∈N*,使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0,n)为函数f(x)的一个“生成点”.则函数f(x)的“生成点”共有( )
A.1个 B.2个 C.3个 D.4个
相关试题

