【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式.
的通项公式.
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]()
![]() 当
当![]() 时,
时, ![]() ,两式相减得
,两式相减得![]()
![]()
![]()
![]() .又当
.又当![]() 时,
时, ![]()
![]()
![]()
![]()
![]()
![]() 是以首项
是以首项![]() ,公比
,公比![]() 的等比数列
的等比数列![]()
![]() 的通项公式为
的通项公式为![]() ;(2)由(1)知,
;(2)由(1)知, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
试题解析: (1)因为![]() ,
,
所以,当![]() 时,
时, ![]() ,................................1分
,................................1分
两式相减得![]() ,即
,即![]() ................3分
................3分
又当![]() 时,
时, ![]() ,即
,即![]() ..........4分
..........4分
所以![]() 是以首项
是以首项![]() ,公比
,公比![]() 的等比数列,
的等比数列,
所以数列![]() 的通项公式为
的通项公式为![]() .......................6分
.......................6分
(2)由(1)知, ![]() ,...................7分
,...................7分
则![]() ,①
,①
![]() ,②.................8分
,②.................8分
②-①得
![]() ,................................10分
,................................10分
![]() ,................................11分
,................................11分
所以,数列![]() 的前
的前![]() 项和为
项和为![]() ..............................12分
..............................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若对于
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)若对于
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列
 中,
中, ,公比
,公比 ,用
,用 表示它的前
表示它的前 项之积:
项之积: ,则
,则 中最大的是( )
中最大的是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
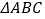 ,
,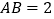 ,
, ,
,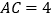 ,点
,点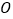 为
为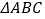 的内心,记
的内心,记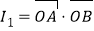 ,
,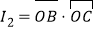 ,
,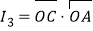 ,则( )
,则( )A.
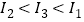 B.
B. 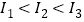 C.
C. 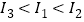 D.
D. 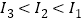
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的对称轴方程;
的对称轴方程;(2)将函数
 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 ,
,  ,
,  分别是
分别是 △三个内角
△三个内角 ,
,  ,
,  的对边,
的对边,  ,
,  ,且
,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
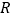 上的函数
上的函数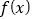 满足
满足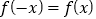 ,且当
,且当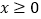 时,
时,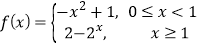 ,若对任意的
,若对任意的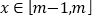 ,不等式
,不等式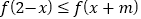 恒成立,则实数
恒成立,则实数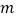 的最大值是( )
的最大值是( )A.
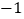 B.
B. 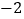 C.
C.  D.
D. 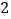
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,动点
,动点 满足
满足 ,且
,且 ,则
,则 在
在 方向上的投影的取值范围是__________.
方向上的投影的取值范围是__________.
相关试题

