【题目】已知动圆过定点，且与定直线相切.

（1）求动圆圆心的轨迹的方程；

（2）若是轨迹的动弦，且过， 分别以、为切点作轨迹的切线，设两切线交点为，证明:.

【答案】（1）（2）详见解析

【解析】

试题（I）由题意可得：动圆圆心到定点（0，2）与到定直线y=-2的距离相等，利用抛物线的定义求轨迹方程即可；（II）设AB：y=kx+2，将直线的方程代入抛物线的方程，消去y得到关于x的一元二次方程，再结合根与系数的关系利用切线的几何意义即可求得过抛物线上A、B两点的切线斜率关系，从而解决问题

试题解析：（1）依题意，圆心的轨迹是以为焦点，为准线的抛物线

因为抛物线焦点到准线距离等于4, 所以圆心的轨迹方程是

（2）

，

，

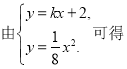
抛物线方程为 所以过抛物线上A、B两点的切线斜率分别是

，.

所以，

(注:也可设,再由,设

则直线AQ:,联立直线和抛物线方程,由直线和抛物线相切得

可得，同理可得，从而证）

关闭