设△ABC的三内角A、B、C成等差数列,sinA、sinB、sinC成等比数列,则这个三角形的形状是
- A.直角三角形
- B.钝角三角形
- C.等腰直角三角形
- D.等边三角形
D
分析:先由△ABC的三内角A、B、C成等差数列,求得∠B=60°,∠A+∠C=120°①;再由sinA、sinB、sinC成等比数列,得sin2B=sinA•sinC,②,①②结合即可判断这个三角形的形状.
解答:∵△ABC的三内角A、B、C成等差数列,
∴∠B=60°,∠A+∠C=120°①;
又sinA、sinB、sinC成等比数列,
∴sin2B=sinA•sinC= ,②
,②
由①②得:sinA•sin(120°-A)
=sinA•(sin120°cosA-cos120°sinA)
= sin2A+
sin2A+ •
•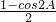
= sin2A-
sin2A- cos2A+
cos2A+
= sin(2A-30°)+
sin(2A-30°)+
= ,
,
∴sin(2A-30°)=1,又0°<∠A<120°
∴∠A=60°.
故选D.
点评:本题考查数列与三角函数的综合,关键在于求得∠B=60°,∠A+∠C=120°,再利用三角公式转化,着重考查分析与转化的能力,属于中档题.
分析:先由△ABC的三内角A、B、C成等差数列,求得∠B=60°,∠A+∠C=120°①;再由sinA、sinB、sinC成等比数列,得sin2B=sinA•sinC,②,①②结合即可判断这个三角形的形状.
解答:∵△ABC的三内角A、B、C成等差数列,
∴∠B=60°,∠A+∠C=120°①;
又sinA、sinB、sinC成等比数列,
∴sin2B=sinA•sinC=
 ,②
,②由①②得:sinA•sin(120°-A)
=sinA•(sin120°cosA-cos120°sinA)
=
 sin2A+
sin2A+ •
•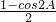
=
 sin2A-
sin2A- cos2A+
cos2A+
=
 sin(2A-30°)+
sin(2A-30°)+
=
 ,
,∴sin(2A-30°)=1,又0°<∠A<120°
∴∠A=60°.
故选D.
点评:本题考查数列与三角函数的综合,关键在于求得∠B=60°,∠A+∠C=120°,再利用三角公式转化,着重考查分析与转化的能力,属于中档题.

