搜索
已知定义域为R的函数y=f（x）满足f（-x）=-f（x+4），当x＞2时，f（x）单调递增，若x1+x2＜4且（x1-2）（x2-2）＜0，则f（x1）+f（x2）的值
- A.恒大于0
- B.恒小于0
- C.可能等于0
- D.可正可负
B
分析：先通过给定条件确定函数为关于点（2，0）成中心对称，再由图象可得答案．
解答：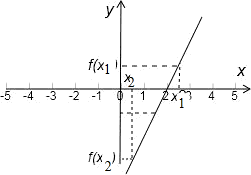
解：由函数y=f（x）满足f（-x）=-f（x+4）得函数的图象关于点（2，0）对称，
由x1+x2＜4且（x1-2）（x2-2）＜0不妨设x1＞2，x2＜2，
借助图象可得f（x1）+f（x2）的值恒小于0，
故选B．
点评：本题主要考查函数的对称性．
分析：先通过给定条件确定函数为关于点（2，0）成中心对称，再由图象可得答案．
解答：
解：由函数y=f（x）满足f（-x）=-f（x+4）得函数的图象关于点（2，0）对称，由x1+x2＜4且（x1-2）（x2-2）＜0不妨设x1＞2，x2＜2，
借助图象可得f（x1）+f（x2）的值恒小于0，
故选B．
点评：本题主要考查函数的对称性．
