【题目】设函数![]()
![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)设![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(3)斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]()
![]() 两点,
两点,
求证:![]()
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上是增函数;当
上是增函数;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在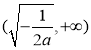 上单调递减;(3)见解析.
上单调递减;(3)见解析.
【解析】
(1)对函数![]() 求导,求其单调区间,即可求出极值,可得最小值;(2)分别讨论
求导,求其单调区间,即可求出极值,可得最小值;(2)分别讨论![]() 和
和![]() 时函数
时函数![]() 的单调性;(3)将直线斜率
的单调性;(3)将直线斜率![]() 用
用![]() 表示出来,将要证的不等式转化为证
表示出来,将要证的不等式转化为证![]() (
(![]() ),最后讨论函数
),最后讨论函数![]() (
(![]() )和
)和![]() (
(![]() )单调性,即可证明原题.
)单调性,即可证明原题.
(1)![]() ,令
,令![]() ,得
,得![]()
因为当![]() 时
时![]() ;当
;当![]() 时
时![]() ,
,
所以当![]() 时,
时,![]()
(2)![]() ,
,![]()
①当![]() 时,恒有
时,恒有![]() ,
,![]() 在
在![]() 上是增函数;
上是增函数;
②当![]() 时,
时,
令![]() ,得
,得![]() ,解得
,解得![]() ;
;
令![]() ,得
,得![]() ,解得
,解得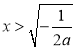 ,
,
综上,当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在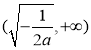 上单调递减
上单调递减
(3) ![]() .
.
要证![]() ,即证
,即证![]() ,等价于证
,等价于证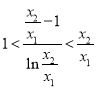 ,令
,令![]() ,
,
则只要证![]() ,由
,由![]() 知
知![]() ,故等价于证
,故等价于证![]() (*).
(*).
① 设![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是增函数,
上是增函数,
∴ 当![]() 时,
时,![]() ,即
,即![]() .
.
② 设![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是增函数,
上是增函数,
∴ 当![]() 时,
时,![]() ,即
,即![]() .
.
由①②知(*)成立,![]() 得证.
得证.

