
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
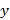
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中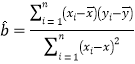
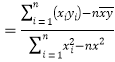 .
.
【答案】(1) ![]() ,
, ![]() 百万元;(2)
百万元;(2) ![]() 型新材料.
型新材料.
【解析】
(1)根据所给的数据,做出变量![]() 的平均数,求出最小二乘法所需要的数据,可得线性回归方程的系数
的平均数,求出最小二乘法所需要的数据,可得线性回归方程的系数![]() ,再根据样本中心点一定在线性回归方程上,求出
,再根据样本中心点一定在线性回归方程上,求出![]() 的值,写出线性回归方程;将
的值,写出线性回归方程;将![]() 代入所求线性回归方程,求出对应的
代入所求线性回归方程,求出对应的![]() 的值即可得结果; (2)求出
的值即可得结果; (2)求出![]() 型新材料对应产品的使用寿命的平均数与
型新材料对应产品的使用寿命的平均数与![]() 型新材料对应产品的使用寿命的平均数,比较其大小即可得结果.
型新材料对应产品的使用寿命的平均数,比较其大小即可得结果.
(1)由折线图可知统计数据![]() 共有
共有![]() 组,
组,
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
计算可得![]() ,
,
![]()
所以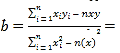
![]() ,
,
![]() ,
,
所以月度利润![]() 与月份代码
与月份代码![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
当![]() 时,
时,![]() .
.
故预计甲公司2019年3月份的利润为![]() 百万元.
百万元.
(2)![]() 型新材料对应产品的使用寿命的平均数为
型新材料对应产品的使用寿命的平均数为![]() ,
,![]() 型新材料对应的产品的使用寿命的平均数为
型新材料对应的产品的使用寿命的平均数为![]() ,
,![]()
![]() 应该采购
应该采购![]() 型新材料.
型新材料.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,设
,设![]() 为线段
为线段![]() 的中点.则在
的中点.则在![]() 翻折过程中,给出如下结论:
翻折过程中,给出如下结论:
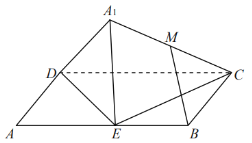
①当![]() 不在平面
不在平面![]() 内时,
内时,![]() 平面
平面![]() ;
;
②存在某个位置,使得![]() ;
;
③线段![]() 的长是定值;
的长是定值;
④当三棱锥![]() 体积最大时,其外接球的表面积为
体积最大时,其外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.(请将所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中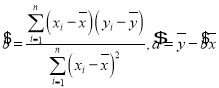 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
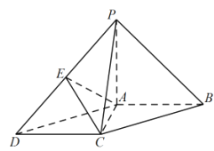
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为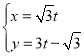 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com