
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,且平面
,且平面![]() 平面
平面![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】【试题分析】(1)连接![]() ,根据菱形的几何性质有
,根据菱形的几何性质有![]() ,由面面垂直的性质定理可知
,由面面垂直的性质定理可知![]() 平面
平面![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .(2) 设
.(2) 设![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,通过计算平面
为坐标原点建立空间直角坐标系,通过计算平面![]() 和平面
和平面![]() 的法向量来求二面角的余弦值.
的法向量来求二面角的余弦值.
【试题解析】
(1)证明:
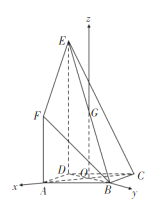
连接![]() ,由四边形
,由四边形![]() 为菱形可知
为菱形可知![]() ,
,
∵平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ;
;
(2)解:设![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,
,
由(1)可知![]() 两两互相垂直,
两两互相垂直,
则可建立如图所示的空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,即
,即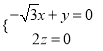 ,
,
取![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
同理可得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
则![]() ,
,
又二面角![]() 的平面角为钝角,则其余弦值为
的平面角为钝角,则其余弦值为![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】(2017·湖北武汉第二次调研)如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35),[35,40),[40,45)的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为 ( )
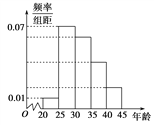
A. 0.04 B. 0.06
C. 0.2 D. 0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘走私船,在
处有一艘走私船,在![]() 处北偏西
处北偏西![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘缉私艇奉命以
处有一艘缉私艇奉命以![]() 海里/时的速度追截走私船,此时,走私船正以
海里/时的速度追截走私船,此时,走私船正以![]() 海里/时的速度从
海里/时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.
方向逃窜.
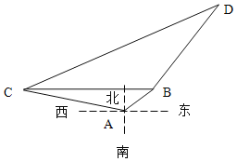
(1)问![]() 船与
船与![]() 船相距多少海里?
船相距多少海里?![]() 船在
船在![]() 船的什么方向?
船的什么方向?
(2)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列的![]() 公差
公差![]() 不为0,
不为0,![]() 是其前
是其前![]() 项和,给出下列命题:
项和,给出下列命题:
①若![]() ,且
,且![]() ,则
,则![]() 和
和![]() 都是
都是![]() 中的最大项;
中的最大项;
②给定![]() ,对一切
,对一切![]() ,都有
,都有![]() ;
;
③若![]() ,则
,则![]() 中一定有最小项;
中一定有最小项;
④存在![]() ,使得
,使得![]() 和
和![]() 同号.
同号.
其中正确命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数,
为参数, ![]() ),将曲线
),将曲线![]() 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线![]() .
.
(1)以原点为极点, ![]() 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() (
(![]() 为参数)与
为参数)与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数,
为参数, ![]() ),将曲线
),将曲线![]() 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线![]() .
.
(1)以原点为极点, ![]() 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() (
(![]() 为参数)与
为参数)与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com