【题目】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.

①求证: ![]() .
.
②求点![]() 到平面
到平面![]() 的距离.
的距离.
③求二面角![]() 的余弦值的大小.
的余弦值的大小.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由等腰三角形得![]() ,由
,由![]() 平面
平面![]() 得
得![]() ,故而可得
,故而可得![]() 平面
平面![]() ,最后得结论;(2)点
,最后得结论;(2)点![]() 到平面
到平面![]() 的距离为
的距离为![]() .通过
.通过![]() 转化
转化![]() ,求点
,求点![]() 到平面
到平面![]() 的距离;(3)以
的距离;(3)以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴,建立空间直角坐标系,求出面
轴,建立空间直角坐标系,求出面![]() 和面
和面![]() 的法向量,计算法向量的夹角,根据图可判断二面角为锐角,故可得角的大小.
的法向量,计算法向量的夹角,根据图可判断二面角为锐角,故可得角的大小.
试题解析:(1)∵在等腰![]() 中,
中, ![]() 为斜边
为斜边![]() 中点,∴
中点,∴![]() ,又∵在直三棱柱
,又∵在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴ ![]() ,∵
,∵![]() 点,
点, ![]() 、
、![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,在三棱锥
,在三棱锥![]() 中,∵
中,∵![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() ,易求得
,易求得![]() ,
, ![]() ,∴
,∴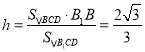 ,即点
,即点![]() 到平面
到平面![]() 的距离是
的距离是![]()
(3)如图,
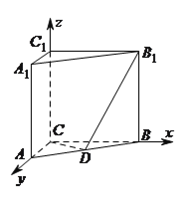
以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .设平面
.设平面![]() 的一个法向量
的一个法向量![]() ,
, ![]() ,
, ![]() ,设平面
,设平面![]() 的一个法向量
的一个法向量![]() ,
, ![]() ,
, ![]() ,∴
,∴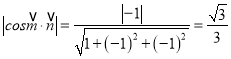 ,由图知,所求二面角为锐角,余弦值为
,由图知,所求二面角为锐角,余弦值为![]() .
.

