【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且其6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为 .
【答案】![]()
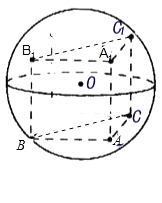
【解析】解:因为三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,
所以三棱柱的底面是直角三角形,侧棱与底面垂直,侧面B1BCC1 , 经过球的球心,球的直径是其对角线的长,
因为AB=3,AC=4,BC=5,BC1= ![]() =13.
=13.
所以球的半径为: ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用球内接多面体的相关知识可以得到问题的答案,需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长.

