17.在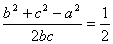 中,
中,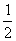 所对的边长分别为
所对的边长分别为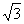 ,设
,设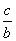 满足条件
满足条件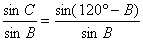 和
和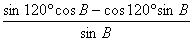 ,求
,求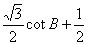 和
和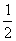 的值.
的值.
17.解法一:由余弦定理
cosA=![]() ,
,
因此,∠A=60°
在△ABC中,∠C=180°-∠A-∠B=120°-∠B。由已知条件,应用正弦定理
![]() +
+![]() =
=![]() =
=![]()
=![]()
=![]() ,
,
解得cot B=2,从而tan B=![]()
解法二:由余弦定理
cos A=![]()
因此,∠A=60°
由 b2+c2-bc=a2,得
(![]() )2=1+(
)2=1+(![]() )2-
)2-![]() =1+
=1+![]() +
+![]() +3-
+3-![]() -
-![]() =
=![]() .
.
所以,![]() =
=![]() , ①
, ①
由正弦定理
sin B=![]() sinA=
sinA=![]() .
.![]() =
=![]()
由①式知a>b,故∠B<∠A,因此∠B为锐角,于是
cosB=![]() =
=![]()
从而 tanB=![]() =
=![]() .
.

