已知向量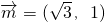 ,向量
,向量 是与向量
是与向量 夹角为
夹角为 的单位向量.
的单位向量.
(1)求向量 ;
;
(2)若向量 与向量
与向量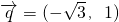 平行,与向量
平行,与向量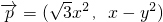 垂直,求t=y2+5x+4的最大值.
垂直,求t=y2+5x+4的最大值.
解:(1)设 =(x,y),
=(x,y),
∵向量 是单位向量,
是单位向量,
∴x2+y2=1.
∵向量 与向量
与向量 夹角为
夹角为 ,
,
∴cos =
=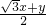 ,
,
∴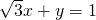 ,
,
解方程组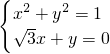 ,
,
得x=0,y=1,或x= ,y=-
,y=- .
.
∴ =(0,1),或
=(0,1),或 =
=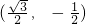 .
.
(2)∵ =(0,1)和向量
=(0,1)和向量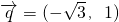 不平行,
不平行,
∴向量 =
=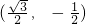 ,
,
向量 与向量
与向量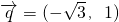 平行,与向量
平行,与向量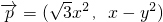 垂直,
垂直,
∴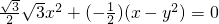 ,
,
∴3x2-x+y2=0.
t=y2+5x+4
=(-3x2+x)+5x+4
=-3x2+6x+4,
因为-3x2+x>0
所以0<x< ,
,
所以当x= 时,t=-3x2+6x+4取最大值tmax=
时,t=-3x2+6x+4取最大值tmax= .
.
分析:(1)设 =(x,y),向量
=(x,y),向量 是单位向量,向量
是单位向量,向量 与向量
与向量 夹角为
夹角为 ,解方程组
,解方程组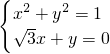 ,能求出
,能求出 =(0,1),或
=(0,1),或 =
=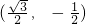 .
.
(2)由 =(0,1)和向量
=(0,1)和向量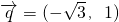 不平行,知向量
不平行,知向量 =
=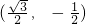 ,由向量
,由向量 与向量
与向量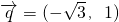 平行,与向量
平行,与向量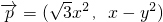 垂直,得到3x2-x+y2=0.所以t=y2+5x+4=-3x2+6x+4,再由导数求t的最大值.
垂直,得到3x2-x+y2=0.所以t=y2+5x+4=-3x2+6x+4,再由导数求t的最大值.
点评:本题考查数量积的性质和应用,解题时要认真审题,注意导数的灵活运用.
 =(x,y),
=(x,y),∵向量
 是单位向量,
是单位向量,∴x2+y2=1.
∵向量
 与向量
与向量 夹角为
夹角为 ,
,∴cos
 =
=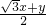 ,
,∴
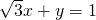 ,
,解方程组
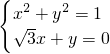 ,
,得x=0,y=1,或x=
 ,y=-
,y=- .
.∴
 =(0,1),或
=(0,1),或 =
=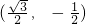 .
.(2)∵
 =(0,1)和向量
=(0,1)和向量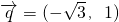 不平行,
不平行,∴向量
 =
=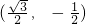 ,
,向量
 与向量
与向量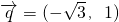 平行,与向量
平行,与向量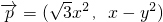 垂直,
垂直,∴
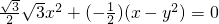 ,
,∴3x2-x+y2=0.
t=y2+5x+4
=(-3x2+x)+5x+4
=-3x2+6x+4,
因为-3x2+x>0
所以0<x<
 ,
,所以当x=
 时,t=-3x2+6x+4取最大值tmax=
时,t=-3x2+6x+4取最大值tmax= .
.分析:(1)设
 =(x,y),向量
=(x,y),向量 是单位向量,向量
是单位向量,向量 与向量
与向量 夹角为
夹角为 ,解方程组
,解方程组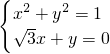 ,能求出
,能求出 =(0,1),或
=(0,1),或 =
=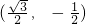 .
.(2)由
 =(0,1)和向量
=(0,1)和向量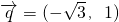 不平行,知向量
不平行,知向量 =
=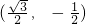 ,由向量
,由向量 与向量
与向量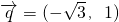 平行,与向量
平行,与向量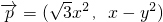 垂直,得到3x2-x+y2=0.所以t=y2+5x+4=-3x2+6x+4,再由导数求t的最大值.
垂直,得到3x2-x+y2=0.所以t=y2+5x+4=-3x2+6x+4,再由导数求t的最大值.点评:本题考查数量积的性质和应用,解题时要认真审题,注意导数的灵活运用.

