【题目】已知椭圆![]() 的长轴为
的长轴为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,若点
,若点![]() 为椭圆
为椭圆![]() 上一动点(不同于点
上一动点(不同于点![]() 、
、![]() )直线
)直线![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 、
、![]() 三点,试问:是否存在实数
三点,试问:是否存在实数![]() ,使得
,使得![]() 恒成立?若存在,请求出实数
恒成立?若存在,请求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
(1)根据长轴长和椭圆上的点的坐标求解标准方程;
(2)求出E,M,F的坐标,根据![]() 建立等量关系分析定值.
建立等量关系分析定值.
(1)因为长轴为![]() ,故
,故![]()
将![]() 代入方程
代入方程![]()
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)①当点![]() 为
为![]() 时,
时,![]() :
:![]() ,
,![]() :
:![]() ,
,![]() :
:![]() 分别与直线
分别与直线![]() 求交点横坐标
求交点横坐标![]() ,
,![]() ,
,![]() ,若满足条件
,若满足条件![]() ,则
,则![]()
解得![]() ;同理,若点
;同理,若点![]() 为
为![]() 时,也解得
时,也解得![]()
②当点![]() 横坐标不为±2,直线
横坐标不为±2,直线![]() :
:![]() 与
与![]() 联立,解得
联立,解得
![]()
直线![]() :
:![]() 与
与![]() 联立,解得
联立,解得
![]()
直线![]() :
:![]() 与
与![]() 联立,解得
联立,解得
![]()
(注:因为直线![]() 与直线
与直线![]() 、
、![]() 、
、![]() 都相交,所以以上分母不为0)
都相交,所以以上分母不为0)
若有![]() ,则
,则![]()
(因为点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,所以当
上,所以当![]() 时,必有
时,必有
![]() ,满足
,满足![]() )
)
故只需验证![]()
![]() ,(*)
,(*)
(若恒成立,取特殊点![]() 代入也满足,得
代入也满足,得
![]()
![]() ,若没有①,此时特殊化得
,若没有①,此时特殊化得![]() 扣2分)
扣2分)
将![]() 代入(*)式验证是否恒成立即可
代入(*)式验证是否恒成立即可
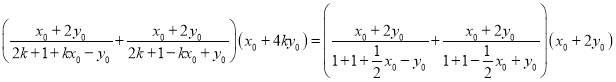
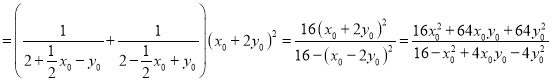
又因为![]() 代入上式,得
代入上式,得
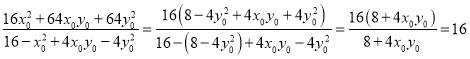 ,
,
即存在![]() ,使得(*)式恒成立.
,使得(*)式恒成立.

