【题目】已知椭圆的离心率是，且椭圆经过点．

（1）求椭圆的标准方程；

（2）若直线： 与圆相切：

（ⅰ）求圆的标准方程；

（ⅱ）若直线过定点，与椭圆交于不同的两点，与圆交于不同的两点，求的取值范围．

【答案】（1）（2），

【解析】试题分析：

（1）由椭圆过点和其离心率可得，故可得椭圆的方程．（2）由题可得直线的斜率存在，设出直线的方程后根据直线与椭圆、圆的位置关系分别求出弦长，求得后根据所得目标函数的特点选择求最值的方法求解即可．

试题解析：

(1) 椭圆经过点，

，解得

，

，解得

∴椭圆的标准方程为

(2) (i)圆的标准方程为,圆心为，

∵直线： 与圆相切，

∴圆的半径,

∴圆的标准方程为．

（ⅱ）由题可得直线的斜率存在,设,

由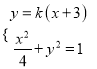消去整理得，

∵直线与椭圆交于不同的两点，

∴，

解得．

设,

则

∴

，

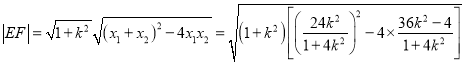
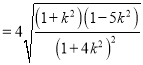又圆的圆心到直线的距离,

∴圆截直线所得弦长,

，

设

则,

,

∵，

∴ ，

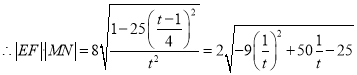∵的取值范围为．

关闭