2025年天利38套高中名校期中期末联考测试卷高中数学必修第一册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套高中名校期中期末联考测试卷高中数学必修第一册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 函数 $ f(x)=\sqrt{2x - 3}+\frac{1}{x - 3} $ 的定义域为(
A.$\left[\frac{3}{2},+\infty\right)$
B.$(-\infty,3)\cup(3,+\infty)$
C.$\left[\frac{3}{2},3\right)\cup(3,+\infty)$
D.$\left(\frac{3}{2},3\right)\cup(3,+\infty)$
C
)A.$\left[\frac{3}{2},+\infty\right)$
B.$(-\infty,3)\cup(3,+\infty)$
C.$\left[\frac{3}{2},3\right)\cup(3,+\infty)$
D.$\left(\frac{3}{2},3\right)\cup(3,+\infty)$
答案:
1. C 函数的定义域 由题知,$\begin{cases}2x - 3 \geq 0, \\x - 3 \neq 0,\end{cases}$解得$x \geq \frac{3}{2}$且$x \neq 3$,即函数$f(x)$的定义域为$[\frac{3}{2},3) \cup (3, +\infty)$,故选C.
2. 下列各组表示同一函数的是(
A.$ f(x)=\sqrt{x^2} $,$ g(x)=\sqrt[3]{x^3} $
B.$ f(x)=1 $,$ g(x)=x^0 $
C.$ f(x)=\begin{cases}x - 2, & x\geq2, \\ -x + 2, & x<2,\end{cases} g(x)=|x - 2| $
D.$ f(x)=x + 3 $,$ g(x)=\frac{x^2 - 9}{x - 3} $
C
)A.$ f(x)=\sqrt{x^2} $,$ g(x)=\sqrt[3]{x^3} $
B.$ f(x)=1 $,$ g(x)=x^0 $
C.$ f(x)=\begin{cases}x - 2, & x\geq2, \\ -x + 2, & x<2,\end{cases} g(x)=|x - 2| $
D.$ f(x)=x + 3 $,$ g(x)=\frac{x^2 - 9}{x - 3} $
答案:
2. C 函数的定义 $f(x)=\sqrt{x^2}=|x|$,$g(x)=\sqrt[3]{x^3}=x$,两者对应关系不同,故不是同一函数,故A不符合题意;$f(x)=1$的定义域为$\mathbf{R}$,$g(x)=x^0$的定义域为$\{x \mid x \neq 0\}$,两者定义域不同,故不是同一函数,故B不符合题意;对于C,$f(x)=\begin{cases}x - 2, & x \geq 2, \\ -x + 2, & x < 2\end{cases}=|x - 2|=g(x)$,两者定义域和对应关系都相同,是同一函数,故C符合题意;对于D,$f(x)=x + 3$的定义域为$\mathbf{R}$,$g(x)=\frac{x^2 - 9}{x - 3}$的定义域为$(-\infty,3) \cup (3, +\infty)$,两者定义域不同,不是同一函数,故D不符合题意,故选C.
3. 已知函数 $ f(x)=\begin{cases}x + 2, & x\leq1, \\ 2x - 3, & x>1,\end{cases}$ 则 $ f(f(1))= $( )
A.1
B.3
C.-3
D.-1
A.1
B.3
C.-3
D.-1
答案:
3. B 分段函数求值 $f(1)=1 + 2 = 3$,$f(f(1))=f(3)=6 - 3 = 3$,故选B.
4. “$\begin{cases}x>1, \\ y>2\end{cases}$”是“$x + y>3$”的( )
A.充要条件
B.充分且不必要条件
C.必要且不充分条件
D.既不充分也不必要条件
A.充要条件
B.充分且不必要条件
C.必要且不充分条件
D.既不充分也不必要条件
答案:
4. B 充分条件与必要条件的判断+不等式的性质 由$\begin{cases}x > 1, \\ y > 2\end{cases}$知$x + y > 3$,故充分性成立;当$x = 0$,$y = 4$时,$x + y > 3$,但$x > 1$不成立,故必要性不成立,故“$\begin{cases}x > 1, \\ y > 2\end{cases}$”是“$x + y > 3$”的充分不必要条件,故选B.
5. 已知函数 $ f(x)=\begin{cases}ax, & x<1, \\ (1 - a)x - 2a, & x\geq1,\end{cases}$ 若函数 $ f(x) $ 在 $ \mathbf{R} $ 上单调递增,则实数 $ a $ 的取值范围是( )
A.$\left(0,\frac{1}{4}\right]$
B.$\left(0,\frac{1}{4}\right)$
C.$\left[\frac{1}{4},1\right)$
D.$\left(\frac{1}{4},1\right)$
A.$\left(0,\frac{1}{4}\right]$
B.$\left(0,\frac{1}{4}\right)$
C.$\left[\frac{1}{4},1\right)$
D.$\left(\frac{1}{4},1\right)$
答案:
5. A 函数的单调性
解法一:由题知,$\begin{cases}a > 0, \\ 1 - a > 0,\end{cases}$(题眼),解得$0 < a \leq \frac{1}{4}$,即实数$a$的取值范围为$(0,\frac{1}{4}]$,故选A.
解法二:当$a = \frac{1}{4}$时,$f(x)=\begin{cases}\frac{1}{4}x, & x < 1, \\ \frac{3}{4}x - \frac{1}{2}, & x \geq 1,\end{cases}$此时函数图象连续,且在$\mathbf{R}$上单调递增,故排除选项B,D;当$a = \frac{1}{2}$时,$f(x)=\begin{cases}\frac{1}{2}x, & x < 1, \\ \frac{1}{2}x - 1, & x \geq 1,\end{cases}$此时函数图象不连续,在$\mathbf{R}$上不单调递增,故排除选项C,故选A.
南京市高一第一学期期中六校联合调研考试(改编)
解法一:由题知,$\begin{cases}a > 0, \\ 1 - a > 0,\end{cases}$(题眼),解得$0 < a \leq \frac{1}{4}$,即实数$a$的取值范围为$(0,\frac{1}{4}]$,故选A.
解法二:当$a = \frac{1}{4}$时,$f(x)=\begin{cases}\frac{1}{4}x, & x < 1, \\ \frac{3}{4}x - \frac{1}{2}, & x \geq 1,\end{cases}$此时函数图象连续,且在$\mathbf{R}$上单调递增,故排除选项B,D;当$a = \frac{1}{2}$时,$f(x)=\begin{cases}\frac{1}{2}x, & x < 1, \\ \frac{1}{2}x - 1, & x \geq 1,\end{cases}$此时函数图象不连续,在$\mathbf{R}$上不单调递增,故排除选项C,故选A.
南京市高一第一学期期中六校联合调研考试(改编)
6. 函数 $ f(x)=\frac{x^4 - 1}{x^2} $ 的图象大致是(
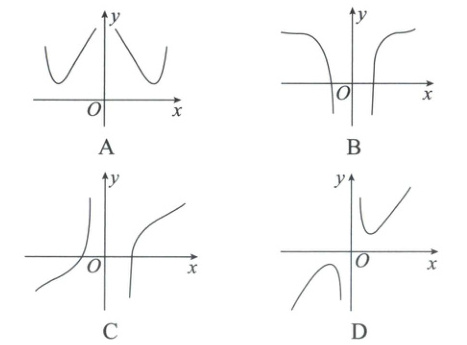
B
)
答案:
6. B 函数图象的判断
通解:因为函数$f(x)=\frac{x^4 - 1}{x^2}$的定义域为$\{x \mid x \neq 0\}$,且$f(-x)=\frac{(-x)^4 - 1}{(-x)^2}=\frac{x^4 - 1}{x^2}=f(x)$(题眼),所以函数$f(x)$为偶函数,其图象关于$y$轴对称,故排除选项C,D;因为$f(1)=0$,故排除选项A,故选B.
快解:由$f(1)=0$排除选项A,D;由$f(-1)=0$,$f(-\frac{1}{2})=-\frac{-\frac{1}{16} - 1}{\frac{1}{4}}=-\frac{-\frac{15}{16}}{\frac{1}{4}}=\frac{15}{4}<0$,排除选项C,故选B.
通解:因为函数$f(x)=\frac{x^4 - 1}{x^2}$的定义域为$\{x \mid x \neq 0\}$,且$f(-x)=\frac{(-x)^4 - 1}{(-x)^2}=\frac{x^4 - 1}{x^2}=f(x)$(题眼),所以函数$f(x)$为偶函数,其图象关于$y$轴对称,故排除选项C,D;因为$f(1)=0$,故排除选项A,故选B.
快解:由$f(1)=0$排除选项A,D;由$f(-1)=0$,$f(-\frac{1}{2})=-\frac{-\frac{1}{16} - 1}{\frac{1}{4}}=-\frac{-\frac{15}{16}}{\frac{1}{4}}=\frac{15}{4}<0$,排除选项C,故选B.
7. 设 $ f(x) $ 是偶函数,且对任意的 $ x_1,x_2\in(-\infty,0)(x_1\neq x_2) $,有 $ (x_1 - x_2)[f(x_1) - f(x_2)]>0 $,$ f(2023)=0 $,则 $ \frac{f(x)+f(-x)}{x}<0 $ 的解集为(
A.$(-\infty,0)\cup(2023,+\infty)$
B.$(-\infty,-2023)\cup(0,2023)$
C.$(-2023,0)\cup(0,2023)$
D.$(-2023,0)\cup(2023,+\infty)$
D
)A.$(-\infty,0)\cup(2023,+\infty)$
B.$(-\infty,-2023)\cup(0,2023)$
C.$(-2023,0)\cup(0,2023)$
D.$(-2023,0)\cup(2023,+\infty)$
答案:
7. D 函数单调性的判断+利用函数的单调性解不等式 对任意的$x_1$,$x_2 \in (-\infty,0)$,不妨设$x_1 < x_2$,则$x_1 - x_2 < 0$,则$f(x_1) - f(x_2) < 0$,即$f(x_1) < f(x_2)$,所以函数$f(x)$在$(-\infty,0)$上为增函数(题眼). 又函数$f(x)$为偶函数,所以$f(x)$在$(0, +\infty)$上为减函数. 又$f(2023)=0$,所以$f(-2023)=f(2023)=0$. 又$\frac{f(x) + f(-x)}{x}=\frac{2f(x)}{x}<0$,当$x < 0$时,$f(x) > 0 = f(-2023)$,所以$-2023 < x < 0$;当$x > 0$时,$f(x) < 0 = f(2023)$,所以$x > 2023$,所以不等式$\frac{f(x) + f(-x)}{x} < 0$的解集为$(-2023,0) \cup (2023, +\infty)$,故选D.
8. 任何正实数 $ N $ 可以表示成 $ N = a×10^n(1\leq a<10,n\in\mathbf{Z}) $,此时 $ \lg N = n + \lg a(0\leq\lg a<1) $,则 $ 2^{-20} $ 在小数点后第几位开始出现非零数字(参考数据:$\lg2\approx0.3010$)(
A.4
B.5
C.6
D.7
D
)A.4
B.5
C.6
D.7
答案:
8. D 对数运算 $\lg 2^{-20} = -20\lg 2 \approx -20 × 0.3010 = -7 + 0.98$,$\therefore n = -7$,$\lg a = 0.98$,$\therefore 2^{-20} \approx 10^{0.98} × 10^{-7}$,$\therefore$在小数点后第7位开始出现非零数字,故选D.
查看更多完整答案,请扫码查看


