2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
知识点1 $\sin \alpha, \cos \alpha$与$\sin\left(\alpha \pm \frac{\pi}{2}\right), \cos\left(\alpha \pm \frac{\pi}{2}\right)$的关系
(1) 如图1,对任意角$\alpha$,有$\sin\left(\alpha + \frac{\pi}{2}\right) = $
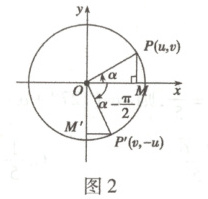
(2) 如图2,对任意角$\alpha$,有$\sin\left(\alpha - \frac{\pi}{2}\right) = $
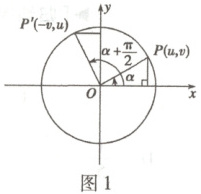
(1) 如图1,对任意角$\alpha$,有$\sin\left(\alpha + \frac{\pi}{2}\right) = $
$\cos \alpha$
$$,$\cos\left(\alpha + \frac{\pi}{2}\right) = $$-\sin \alpha$
$$.(2) 如图2,对任意角$\alpha$,有$\sin\left(\alpha - \frac{\pi}{2}\right) = $
$-\cos \alpha$
$$,$\cos\left(\alpha - \frac{\pi}{2}\right) = $$\sin \alpha$
$$.

答案:
知识点1
(1)$\cos \alpha$ $-\sin \alpha$
(2)$-\cos \alpha$ $\sin \alpha$
(1)$\cos \alpha$ $-\sin \alpha$
(2)$-\cos \alpha$ $\sin \alpha$
知识点2 正弦函数、余弦函数的诱导公式
对任意角$\alpha$,下列关系式成立(其中$k \in \mathbf{Z}$).
$\sin(\alpha + 2k\pi) = $$$,$\cos(\alpha + 2k\pi) = $_________$$,$\sin(-\alpha) = $_________$$,$\cos(-\alpha) = $_________$$,$\sin(\alpha + \pi) = $_________$$,$\cos(\alpha + \pi) = \cos(\pi + \alpha) = $_________$$,$\sin(\alpha - \pi) = $_________$$,$\cos(\alpha - \pi) = $_________$$,$\sin(\pi - \alpha) = $_________$$,$\cos(\pi - \alpha) = $_________$$,$\sin\left(\alpha + \frac{\pi}{2}\right) = \sin\left(\frac{\pi}{2} + \alpha\right) = $_________$$,$\cos\left(\alpha + \frac{\pi}{2}\right) = \cos\left(\frac{\pi}{2} + \alpha\right) = $_________$$,$\sin\left(\frac{\pi}{2} - \alpha\right) = $_________$$,$\cos\left(\frac{\pi}{2} - \alpha\right) = $_________$$.
对任意角$\alpha$,下列关系式成立(其中$k \in \mathbf{Z}$).
$\sin(\alpha + 2k\pi) = $$$,$\cos(\alpha + 2k\pi) = $_________$$,$\sin(-\alpha) = $_________$$,$\cos(-\alpha) = $_________$$,$\sin(\alpha + \pi) = $_________$$,$\cos(\alpha + \pi) = \cos(\pi + \alpha) = $_________$$,$\sin(\alpha - \pi) = $_________$$,$\cos(\alpha - \pi) = $_________$$,$\sin(\pi - \alpha) = $_________$$,$\cos(\pi - \alpha) = $_________$$,$\sin\left(\alpha + \frac{\pi}{2}\right) = \sin\left(\frac{\pi}{2} + \alpha\right) = $_________$$,$\cos\left(\alpha + \frac{\pi}{2}\right) = \cos\left(\frac{\pi}{2} + \alpha\right) = $_________$$,$\sin\left(\frac{\pi}{2} - \alpha\right) = $_________$$,$\cos\left(\frac{\pi}{2} - \alpha\right) = $_________$$.
答案:
知识点2 $\sin \alpha$ $\cos \alpha$ $-\sin \alpha$ $\cos \alpha$ $-\sin \alpha$ $-\cos \alpha$ $\sin \alpha$ $-\cos \alpha$ $\sin \alpha$ $-\cos \alpha$ $\cos \alpha$ $-\sin \alpha$ $\cos \alpha$ $\sin \alpha$
知识点3 诱导公式的记忆方法
诱导公式可以统一概括为“$k · \frac{\pi}{2} \pm \alpha(k \in \mathbf{Z})$”的诱导公式. 当$k$为偶数时,函数名不改变;当$k$为奇数时,函数名改变,然后前面加一个把$\alpha$视为锐角时原函数值的符号. 记忆口诀为“奇变偶不变,符号看象限”.
诱导公式可以统一概括为“$k · \frac{\pi}{2} \pm \alpha(k \in \mathbf{Z})$”的诱导公式. 当$k$为偶数时,函数名不改变;当$k$为奇数时,函数名改变,然后前面加一个把$\alpha$视为锐角时原函数值的符号. 记忆口诀为“奇变偶不变,符号看象限”.
答案:
无(本题为知识点阐述,非解答题,无具体答案选项)
例1. 计算:
(1)$\sin^2 120° + \cos 180° - \cos^2(-330°) + \sin(-210°)$;
(2)$\frac{\sqrt{1 + \cos 100° \sin 170°}}}{\cos 370° + \sqrt{1 - \sin^2 170°}}$
【分析】 利用诱导公式,先化简再求值.
(1)$\sin^2 120° + \cos 180° - \cos^2(-330°) + \sin(-210°)$;
(2)$\frac{\sqrt{1 + \cos 100° \sin 170°}}}{\cos 370° + \sqrt{1 - \sin^2 170°}}$
【分析】 利用诱导公式,先化简再求值.
答案:
例1:
(1)原式$=\sin^260° - \cos 0° - \cos^230° + \sin30° = \frac{3}{4}-1$
$\frac{3}{4}+\frac{1}{2}=-\frac{1}{2}$
(2)原式$=\frac{\sqrt{1+\cos(180° - 80°)\sin(90° + 80°)}}{\cos(360° + 10°) + \sqrt{1 - \sin^2(180° - 10°)}}$
$=\frac{\sqrt{1+(-\cos 80°)\cos 80°}}{\cos 10° + \sqrt{1 - \sin^210°}} = \frac{\sqrt{1-\cos^280°}}{2\cos 10°}$
$=\frac{\sin 80°}{2\cos 10°}=\frac{\cos 10°}{2\cos 10°}=\frac{1}{2}$
(1)原式$=\sin^260° - \cos 0° - \cos^230° + \sin30° = \frac{3}{4}-1$
$\frac{3}{4}+\frac{1}{2}=-\frac{1}{2}$
(2)原式$=\frac{\sqrt{1+\cos(180° - 80°)\sin(90° + 80°)}}{\cos(360° + 10°) + \sqrt{1 - \sin^2(180° - 10°)}}$
$=\frac{\sqrt{1+(-\cos 80°)\cos 80°}}{\cos 10° + \sqrt{1 - \sin^210°}} = \frac{\sqrt{1-\cos^280°}}{2\cos 10°}$
$=\frac{\sin 80°}{2\cos 10°}=\frac{\cos 10°}{2\cos 10°}=\frac{1}{2}$
查看更多完整答案,请扫码查看


