2025年成才之路高中新课程学习指导高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例$2$. (1)已知$f(x)$的导函数$f^{\prime}(x)$的图象如图所示,那么$f(x)$的图象最有可能是图中的 (
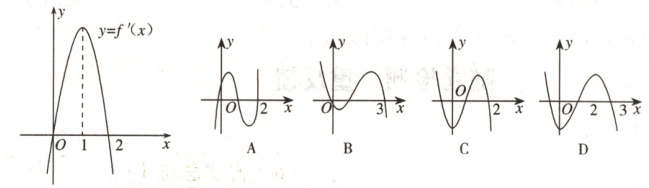
A.
B.
C.
D.
D
)
A.
B.
C.
D.
答案:
例2:
(1) D
【解析】
(1)由题意可知,当$ x\lt0 $和$ x\gt2 $时,导函数$ f'(x)\lt0 $,函数$ f(x) $是减函数;当$ x\in(0,2) $时,导函数$ f'(x)\gt0 $,函数$ f(x) $是增函数,D符合.
(1) D
【解析】
(1)由题意可知,当$ x\lt0 $和$ x\gt2 $时,导函数$ f'(x)\lt0 $,函数$ f(x) $是减函数;当$ x\in(0,2) $时,导函数$ f'(x)\gt0 $,函数$ f(x) $是增函数,D符合.
(2)函数$f(x)$的图象如图所示,设$f(x)$的导函数为$f^{\prime}(x)$,则$\frac{f^{\prime}(x)}{f(x)}>0$的解集为 (
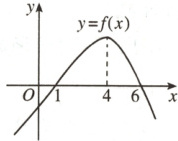
A.$(1,6)$
B.$(1,4)$
C.$(-\infty,1)\cup(6,+\infty)$
D.$(1,4)\cup(6,+\infty)$ [方法总结$2$]
D
)
A.$(1,6)$
B.$(1,4)$
C.$(-\infty,1)\cup(6,+\infty)$
D.$(1,4)\cup(6,+\infty)$ [方法总结$2$]
答案:
例2:
(2) D
【解析】
(2)由题意,$ \frac{f'(x)}{f(x)}\gt0\Rightarrow f'(x)· f(x)\gt0 $,又因为,由图可知,当$ x\in(-\infty,4) $时$ f'(x)\gt0,f(x) $单调递增;当$ x\in(4,+\infty) $时$ f'(x)\lt0,f(x) $单调递减;所以①当$ x\in(1,4) $时$ f'(x)\gt0 $且$ f(x)\gt0 $,②当$ x\in(6,+\infty) $时$ f'(x)\lt0 $且$ f(x)\lt0 $;综上,$ x\in(1,4)\cup(6,+\infty) $.故选 D.
(2) D
【解析】
(2)由题意,$ \frac{f'(x)}{f(x)}\gt0\Rightarrow f'(x)· f(x)\gt0 $,又因为,由图可知,当$ x\in(-\infty,4) $时$ f'(x)\gt0,f(x) $单调递增;当$ x\in(4,+\infty) $时$ f'(x)\lt0,f(x) $单调递减;所以①当$ x\in(1,4) $时$ f'(x)\gt0 $且$ f(x)\gt0 $,②当$ x\in(6,+\infty) $时$ f'(x)\lt0 $且$ f(x)\lt0 $;综上,$ x\in(1,4)\cup(6,+\infty) $.故选 D.
跟踪训练$2$
已知函数$y = f(x)$的导函数$y = f^{\prime}(x)$的图象如图所示,则该函数的图象可能是 (
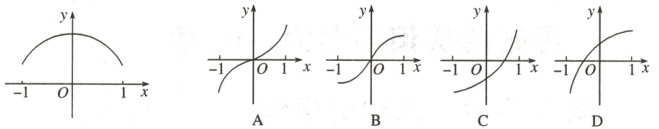
A.
B.
C.
D.
已知函数$y = f(x)$的导函数$y = f^{\prime}(x)$的图象如图所示,则该函数的图象可能是 (
B
)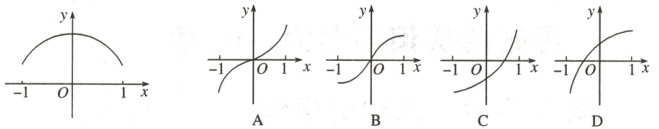
A.
B.
C.
D.
答案:
跟踪训练2:B 由$ y = f'(x) $的图象知,$ y = f(x) $为增函数,且在区间$ (-1,0) $上增长速度越来越快,而在区间$ (0,1) $上增长速度越来越慢,故选 B.
例$3$. 求下列函数的单调区间:
(1)$f(x)=x^{3}-4x^{2}+4x - 1$;
(2)$f(x)=\frac{\mathrm{e}^{x}}{x - 2}$ [方法总结$3$]
(1)$f(x)=x^{3}-4x^{2}+4x - 1$;
(2)$f(x)=\frac{\mathrm{e}^{x}}{x - 2}$ [方法总结$3$]
答案:
例3:【解析】
(1)函数$ f(x) $的定义域为$ \mathbf{R} $,
$ f'(x)=3x^{2}-8x + 4 $.
令$ 3x^{2}-8x + 4 = 0 $,
解得$ x=\frac{2}{3} $或$ x = 2 $.
当$ x $变化时,$ f'(x) $与$ f(x) $的变化情况如下表:
| $ x $ | $ \left(-\infty,\frac{2}{3}\right) $ | $ \frac{2}{3} $ | $ \left(\frac{2}{3},2\right) $ | $ 2 $ | $ (2,+\infty) $ |
| --- | --- | --- | --- | --- | --- |
| $ f'(x) $ | $ + $ | $ 0 $ | $ - $ | $ 0 $ | $ + $ |
| $ f(x) $ | 单调递增 | $ f\left(\frac{2}{3}\right)=\frac{5}{27} $ | 单调递减 | $ f(2)=-1 $ | 单调递增 |
所以函数$ f(x) $的单调递增区间为$ \left(-\infty,\frac{2}{3}\right) $和$ (2,+\infty) $,
单调递减区间为$ \left(\frac{2}{3},2\right) $.
(2)函数$ f(x) $的定义域为$ (-\infty,2)\cup(2,+\infty) $.
$ f'(x)=\frac{\mathrm{e}^{x}(x - 2)-\mathrm{e}^{x}}{(x - 2)^{2}}=\frac{\mathrm{e}^{x}(x - 3)}{(x - 2)^{2}} $.
令$ f'(x)=0 $可得$ x = 3 $,当$ x $变化时,$ f'(x) $与$ f(x) $的变化情况如下表所示:
| $ x $ | $ (-\infty,2) $ | $ (2,3) $ | $ 3 $ | $ (3,+\infty) $ |
| --- | --- | --- | --- | --- |
| $ f'(x) $ | $ - $ | $ - $ | $ 0 $ | $ + $ |
| $ f(x) $ | 单调递减 | 单调递减 | $ f(3)=\mathrm{e}^{3} $ | 单调递增 |
所以函数$ f(x) $的单调递增区间为$ (3,+\infty) $,单调递减区间为$ (-\infty,2) $和$ (2,3) $.
(1)函数$ f(x) $的定义域为$ \mathbf{R} $,
$ f'(x)=3x^{2}-8x + 4 $.
令$ 3x^{2}-8x + 4 = 0 $,
解得$ x=\frac{2}{3} $或$ x = 2 $.
当$ x $变化时,$ f'(x) $与$ f(x) $的变化情况如下表:
| $ x $ | $ \left(-\infty,\frac{2}{3}\right) $ | $ \frac{2}{3} $ | $ \left(\frac{2}{3},2\right) $ | $ 2 $ | $ (2,+\infty) $ |
| --- | --- | --- | --- | --- | --- |
| $ f'(x) $ | $ + $ | $ 0 $ | $ - $ | $ 0 $ | $ + $ |
| $ f(x) $ | 单调递增 | $ f\left(\frac{2}{3}\right)=\frac{5}{27} $ | 单调递减 | $ f(2)=-1 $ | 单调递增 |
所以函数$ f(x) $的单调递增区间为$ \left(-\infty,\frac{2}{3}\right) $和$ (2,+\infty) $,
单调递减区间为$ \left(\frac{2}{3},2\right) $.
(2)函数$ f(x) $的定义域为$ (-\infty,2)\cup(2,+\infty) $.
$ f'(x)=\frac{\mathrm{e}^{x}(x - 2)-\mathrm{e}^{x}}{(x - 2)^{2}}=\frac{\mathrm{e}^{x}(x - 3)}{(x - 2)^{2}} $.
令$ f'(x)=0 $可得$ x = 3 $,当$ x $变化时,$ f'(x) $与$ f(x) $的变化情况如下表所示:
| $ x $ | $ (-\infty,2) $ | $ (2,3) $ | $ 3 $ | $ (3,+\infty) $ |
| --- | --- | --- | --- | --- |
| $ f'(x) $ | $ - $ | $ - $ | $ 0 $ | $ + $ |
| $ f(x) $ | 单调递减 | 单调递减 | $ f(3)=\mathrm{e}^{3} $ | 单调递增 |
所以函数$ f(x) $的单调递增区间为$ (3,+\infty) $,单调递减区间为$ (-\infty,2) $和$ (2,3) $.
查看更多完整答案,请扫码查看


