《2025年成才之路高中新课程学习指导高中数学选择性必修第二册人教版》

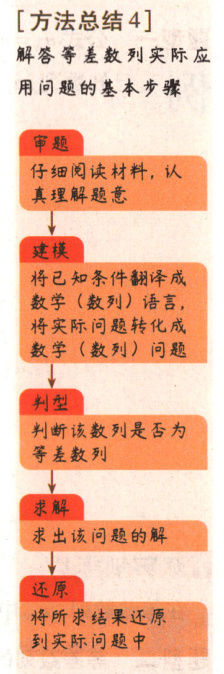
例4. 有一批电视机原销售价为每台$800$元，在甲、乙两家家电商场均有销售.甲商场用如下方法促销：买一台单价为$780$元，买两台单价为$760$元，以此类推，每多买一台则所购买各台的单价均减少$20$元，但每台最少不低于$440$元;乙商场一律按原价的$75\%$销售.某单位需购买一批此类电视机，则去哪一家商场购买花费较少? [方法总结$4$]

答案： 例4：【解析】 设某单位需购买电视机$n$台。
在甲商场购买时，所购买电视机的售价构成等差数列$\{a_{n}\}$，$a_{n} = 780 + (n - 1)×(-20) = -20n + 800$，
由$a_{n} = -20n + 800 \geq 440$，得$n \leq 18$，
即购买台数不超过$18$台时，每台售价$(800 - 20n)$元；
购买台数超过$18$台时，每台售价$440$元。
到乙商场购买时，每台售价为$800×75\% = 600$（元）。
比较在甲、乙两家家电商场的费用
$(800 - 20)n - 600n = 20n(10 - n)$。
当$n ＜ 10$时，$(800 - 20n)n ＞ 600n$，到乙商场购买花费较少；
当$n = 10$时，$(800 - 20n)n = 600n$，到甲、乙商场购买花费相同；
当$10 ＜ n \leq 18$时，$(800 - 20n)n ＜ 600n$，到甲商场购买花费较少；
当$n ＞ 18$时，$440n ＜ 600n$，到甲商场购买花费较少。
因此，当购买电视机台数少于$10$台时，到乙商场购买花费较少；当购买电视机$10$台时，到两家商场购买花费相同；当购买电视机台数多于$10$台时，到甲商场购买花费较少。

跟踪训练4
某公司$2024$年经销一种数码产品，获利$200$万元，从$2025$年起，预计其利润每年比上一年减少$20$万元.按照这一规律，如果该公司不开发新产品，也不调整经营策略，从哪一年起，该公司经销这一产品将出现亏损?

答案： 跟踪训练4：【解析】 记2024年为第1年，由题设可知第1年获利200万元，第2年获利180万元，第3年获利160万元，$·s·s$，则每年获利构成等差数列$\{a_{n}\}$，且当$a_{n} ＜ 0$时，该公司经销此产品将出现亏损。
设第$n$年的利润为$a_{n}$，因为$a_{1} = 200$，公差$d = -20$，所以$a_{n} = a_{1} + (n - 1)d = 220 - 20n$。
由题意知，数列$\{a_{n}\}$为递减数列，令$a_{n} ＜ 0$，即$a_{n} = 220 - 20n ＜ 0$，解得$n ＞ 11$，即从第12年起，也就是从2035年开始，该公司经销此产品将出现亏损。