1.先过下面的点A画一条射线,然后在这条射线上截取一段4厘米长的线段AB。
A·
A·
答案:
1. 以点 A 为起点,向某一方向画一条射线;
2. 在射线上从点 A 开始,用直尺量取 4 厘米的长度,标记点 B;
3. 最终得到线段 AB 长度为 4 厘米。
2. 在射线上从点 A 开始,用直尺量取 4 厘米的长度,标记点 B;
3. 最终得到线段 AB 长度为 4 厘米。
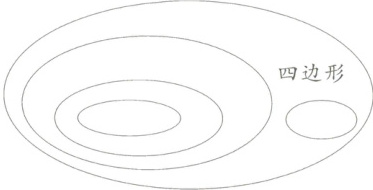
2.根据多边形之间的关系,将“长方形”“正方形”“平行四边形”“梯形”填入图中相应的位置。

答案:
最外层:四边形
从外往里第二层:平行四边形,梯形
从外往里第三层:长方形
最里层:正方形
从外往里第二层:平行四边形,梯形
从外往里第三层:长方形
最里层:正方形
3.不测量,将角和对应角度用线连接起来。
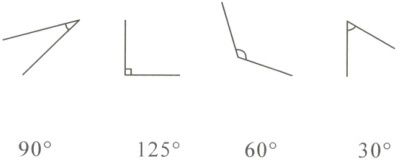
$90°$ $125°$ $60°$ $30°$

$90°$ $125°$ $60°$ $30°$
答案:
90° —— 第二个图;125° —— 第一个图;60° —— 第三个图;30° —— 第四个图。
4.求图中指定角的度数。
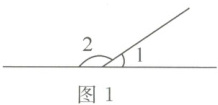
(1)如图1,已知$∠1=35°$,则$∠2=$
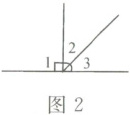
(2)如图2,已知$∠1=90°$,$∠2=45°$,则$∠3=$
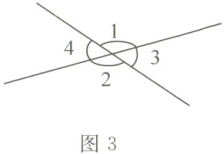
(3)如图3,已知$∠1=130°$,则$∠2=$
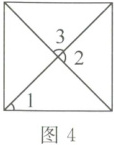
(4)如图4,是一个正方形,则$∠1=$
(1)如图1,已知$∠1=35°$,则$∠2=$
$145^{\circ}$
。(2)如图2,已知$∠1=90°$,$∠2=45°$,则$∠3=$
$45^{\circ}$
。(3)如图3,已知$∠1=130°$,则$∠2=$
$50^{\circ}$
,$∠3=$$130^{\circ}$
,$∠4=$$50^{\circ}$
。(4)如图4,是一个正方形,则$∠1=$
$90^{\circ}$
,$∠2=$$90^{\circ}$
,$∠3=$$45^{\circ}$
。



答案:
(1) $180^{\circ}-35^{\circ}=145^{\circ}$,故$\angle2 = 145^{\circ}$。
(2) 因为$\angle1$是直角为$90^{\circ}$,$\angle1+\angle2+\angle3 = 180^{\circ}$(平角),所以$\angle3=180^{\circ}-\angle1-\angle2=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$。
(3) $\angle1$和$\angle2$组成平角,所以$\angle2=180^{\circ}-\angle1=180^{\circ}-130^{\circ}=50^{\circ}$;$\angle1$和$\angle3$是对顶角,对顶角相等,所以$\angle3=\angle1 = 130^{\circ}$;$\angle2$和$\angle4$是对顶角,所以$\angle4=\angle2 = 50^{\circ}$。
(4) 正方形的四个角都是直角,所以$\angle1 = 90^{\circ}$;正方形的对角线互相垂直,所以$\angle2 = 90^{\circ}$;对角线平分内角,正方形内角为$90^{\circ}$,所以$\angle3=90^{\circ}÷2 = 45^{\circ}$。
(1) $145^{\circ}$
(2) $45^{\circ}$
(3) $50^{\circ}$,$130^{\circ}$,$50^{\circ}$
(4) $90^{\circ}$,$90^{\circ}$,$45^{\circ}$
(1) $180^{\circ}-35^{\circ}=145^{\circ}$,故$\angle2 = 145^{\circ}$。
(2) 因为$\angle1$是直角为$90^{\circ}$,$\angle1+\angle2+\angle3 = 180^{\circ}$(平角),所以$\angle3=180^{\circ}-\angle1-\angle2=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$。
(3) $\angle1$和$\angle2$组成平角,所以$\angle2=180^{\circ}-\angle1=180^{\circ}-130^{\circ}=50^{\circ}$;$\angle1$和$\angle3$是对顶角,对顶角相等,所以$\angle3=\angle1 = 130^{\circ}$;$\angle2$和$\angle4$是对顶角,所以$\angle4=\angle2 = 50^{\circ}$。
(4) 正方形的四个角都是直角,所以$\angle1 = 90^{\circ}$;正方形的对角线互相垂直,所以$\angle2 = 90^{\circ}$;对角线平分内角,正方形内角为$90^{\circ}$,所以$\angle3=90^{\circ}÷2 = 45^{\circ}$。
(1) $145^{\circ}$
(2) $45^{\circ}$
(3) $50^{\circ}$,$130^{\circ}$,$50^{\circ}$
(4) $90^{\circ}$,$90^{\circ}$,$45^{\circ}$
查看更多完整答案,请扫码查看


