2025年金版新学案高三总复习数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高三总复习数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
2. (链接北师必修二 $P26A$ 组 $T7$,改编)已知角 $\alpha$ 的终边经过点 $P(1, -2)$,则 $\sin \alpha =$(
A.$\frac{\sqrt{5}}{5}$
B.$-\frac{2\sqrt{5}}{5}$
C.$-2$
D.$-\frac{1}{2}$
B
)A.$\frac{\sqrt{5}}{5}$
B.$-\frac{2\sqrt{5}}{5}$
C.$-2$
D.$-\frac{1}{2}$
答案:
2.B 角α的终边经过点P(1,−2),则r = |OP| = $\sqrt{1^{2}+(-2)^{2}}$ = $\sqrt{5}$,所以$\sin\alpha = \frac{-2}{\sqrt{5}} = -\frac{2\sqrt{5}}{5}$,故选B。
3. (链接北师必修二 $P12A$ 组 $T3$,改编)若 $\alpha = 6$,则角 $\alpha$ 的终边在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
3.D $\alpha - 2\pi = 6 - 2\pi \in (-\frac{\pi}{2},0)$,故角α的终边在第四象限,故选D。
4. (链接北师必修二 $P12$ 练习 $T8$,改编)已知扇形的圆心角为 $30^{\circ}$,其弧长为 $2\pi$,则此扇形的面积为
12π
.
答案:
4.12π 因为$\alpha = 30^{\circ} = \frac{\pi}{6}$,$l = \alpha r$,所以$r = \frac{2\pi}{\frac{\pi}{6}} = 12$,所以扇形面积$S = \frac{1}{2}lr = \frac{1}{2} × 2\pi × 12 = 12\pi$。
1. (多选题)下列说法正确的是(
A.如果 $\alpha$ 是第一象限的角,则 $-\alpha$ 是第四象限的角
B.角 $\frac{\pi}{3}$ 与角 $\frac{2}{3}\pi$ 的终边与单位圆的交点关于 $y$ 轴对称
C.终边落在 $y$ 轴上的角的集合可表示为 $\{ \alpha | \alpha = 90^{\circ} + k\pi, k \in \mathbf{Z} \}$
D.若 $\alpha$ 是第二象限角,则点 $P(\sin \alpha, \cos \alpha)$ 在第四象限
ABD
)A.如果 $\alpha$ 是第一象限的角,则 $-\alpha$ 是第四象限的角
B.角 $\frac{\pi}{3}$ 与角 $\frac{2}{3}\pi$ 的终边与单位圆的交点关于 $y$ 轴对称
C.终边落在 $y$ 轴上的角的集合可表示为 $\{ \alpha | \alpha = 90^{\circ} + k\pi, k \in \mathbf{Z} \}$
D.若 $\alpha$ 是第二象限角,则点 $P(\sin \alpha, \cos \alpha)$ 在第四象限
答案:
1.ABD 对于A,α是第一象限的角,即$2k\pi < \alpha < \frac{\pi}{2} + 2k\pi$,$k \in \mathbf{Z}$,则$-\frac{\pi}{2} - 2k\pi < -\alpha < -2k\pi$,$k \in \mathbf{Z}$,因此−α是第四象限的角,故A正确;对于B,由角的终边易知角$\frac{\pi}{3}$与角$\frac{2\pi}{3}$的终边关于y轴对称,故B正确;对于C,出现角度制与弧度制混用错误,故C错误;对于D,由α是第二象限角,得$\sin\alpha > 0$,$\cos\alpha < 0$,则点P($\sin\alpha$,$\cos\alpha$)在第四象限,故D正确,故选ABD。
2. (2025·湖北武汉模拟)若角 $\alpha$ 的顶点为坐标原点,始边在 $x$ 轴的非负半轴上,终边在直线 $y = \sqrt{3}x$ 上,则角 $\alpha$ 的取值集合是(
A.$\{ \alpha | \alpha = 2k\pi + \frac{\pi}{3}, k \in \mathbf{Z} \}$
B.$\{ \alpha | \alpha = 2k\pi + \frac{2\pi}{3}, k \in \mathbf{Z} \}$
C.$\{ \alpha | \alpha = k\pi + \frac{2\pi}{3}, k \in \mathbf{Z} \}$
D.$\{ \alpha | \alpha = k\pi + \frac{\pi}{3}, k \in \mathbf{Z} \}$
D
)A.$\{ \alpha | \alpha = 2k\pi + \frac{\pi}{3}, k \in \mathbf{Z} \}$
B.$\{ \alpha | \alpha = 2k\pi + \frac{2\pi}{3}, k \in \mathbf{Z} \}$
C.$\{ \alpha | \alpha = k\pi + \frac{2\pi}{3}, k \in \mathbf{Z} \}$
D.$\{ \alpha | \alpha = k\pi + \frac{\pi}{3}, k \in \mathbf{Z} \}$
答案:
2.D 根据题意,角α的终边在直线$y = \sqrt{3}x$上,α为第一象限角时,$\alpha = \frac{\pi}{3} + 2k\pi$($k \in \mathbf{Z}$);α为第三象限角时,$\alpha = \frac{4\pi}{3} + 2k\pi$($k \in \mathbf{Z}$);综上,角α的取值集合是{$\alpha \mid \alpha = k\pi + \frac{\pi}{3}$,$k \in \mathbf{Z}$},故选D。
3. 如图,终边落在阴影部分(包括边界)的角 $\alpha$ 的集合是(
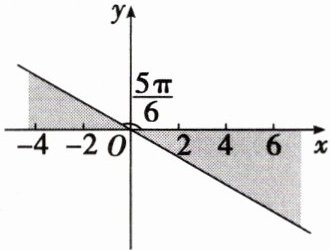
A.$\{ \alpha | \frac{5\pi}{6} + 2k\pi \leq \alpha \leq (2k + 1)\pi, k \in \mathbf{Z} \}$
B.$\{ \alpha | \frac{5\pi}{6} + k\pi \leq \alpha \leq (k + 1)\pi, k \in \mathbf{Z} \}$
C.$\{ \alpha | -\frac{7\pi}{6} + 2k\pi \leq \alpha \leq (2k - 1)\pi, k \in \mathbf{Z} \}$
D.$\{ \alpha | -\frac{\pi}{6} + 2k\pi \leq \alpha \leq 2k\pi, k \in \mathbf{Z} \}$
B
)
A.$\{ \alpha | \frac{5\pi}{6} + 2k\pi \leq \alpha \leq (2k + 1)\pi, k \in \mathbf{Z} \}$
B.$\{ \alpha | \frac{5\pi}{6} + k\pi \leq \alpha \leq (k + 1)\pi, k \in \mathbf{Z} \}$
C.$\{ \alpha | -\frac{7\pi}{6} + 2k\pi \leq \alpha \leq (2k - 1)\pi, k \in \mathbf{Z} \}$
D.$\{ \alpha | -\frac{\pi}{6} + 2k\pi \leq \alpha \leq 2k\pi, k \in \mathbf{Z} \}$
答案:
3.B 终边落在阴影部分的角为$\frac{5\pi}{6} + k\pi \leqslant \alpha \leqslant (k + 1)\pi$,$k \in \mathbf{Z}$,即终边落在阴影部分(包括边界)的角α的集合是{$\alpha \mid \frac{5\pi}{6} + k\pi \leqslant \alpha \leqslant (k + 1)\pi$,$k \in \mathbf{Z}$},故选B。
4. 已知角 $\alpha$ 是第二象限角,且 $| \cos \frac{\alpha}{2} | = \cos \frac{\alpha}{2}$,则角 $\frac{\alpha}{2}$ 是(
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
A
)A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
答案:
4.A 因为角α是第二象限角,所以$\frac{\pi}{2} + 2k\pi < \alpha < \pi + 2k\pi$($k \in \mathbf{Z}$),所以$\frac{\pi}{4} + k\pi < \frac{\alpha}{2} < \frac{\pi}{2} + k\pi$($k \in \mathbf{Z}$),所以角$\frac{\alpha}{2}$是第一象限角或第三象限角。又因为$\cos\frac{\alpha}{2} = \cos\frac{\alpha}{2}$,即$\cos\frac{\alpha}{2} > 0$,所以角$\frac{\alpha}{2}$是第一象限角,故选A。
(1)若 $\alpha = 60^{\circ}$,$r = 3$,求扇形的弧长;
答案:
(1)设扇形的弧长为l。因为$\alpha = 60^{\circ}$,即$\alpha = \frac{\pi}{3}$,$r = 3$,所以$l = \alpha r = \frac{\pi}{3} × 3 = \pi$。
(1)设扇形的弧长为l。因为$\alpha = 60^{\circ}$,即$\alpha = \frac{\pi}{3}$,$r = 3$,所以$l = \alpha r = \frac{\pi}{3} × 3 = \pi$。
(2)若扇形的周长为 $16$,当 $\alpha$ 为多少弧度时,该扇形面积最大?并求出最大面积;
答案:
(2)由题设条件知,$l + 2r = 16$,$l = 16 - 2r$($0 < r < 8$),因此扇形的面积$S = \frac{1}{2}lr = \frac{1}{2}(16 - 2r)r = -r^{2} + 8r = -(r - 4)^{2} + 16$,所以当$r = 4$时,S有最大值16,此时$l = 16 - 2r = 8$,$\alpha = \frac{l}{r} = 2$,所以当$\alpha = 2$时,扇形的面积最大,最大面积是16。
(2)由题设条件知,$l + 2r = 16$,$l = 16 - 2r$($0 < r < 8$),因此扇形的面积$S = \frac{1}{2}lr = \frac{1}{2}(16 - 2r)r = -r^{2} + 8r = -(r - 4)^{2} + 16$,所以当$r = 4$时,S有最大值16,此时$l = 16 - 2r = 8$,$\alpha = \frac{l}{r} = 2$,所以当$\alpha = 2$时,扇形的面积最大,最大面积是16。
(3)若 $\alpha = \frac{\pi}{3}$,$r = 2 cm$,求扇形的弧所在的弓形的面积.
答案:
(3)设弓形面积为$S_{弓形}$,由题意知$l = \frac{2\pi}{3} cm$,所以$S_{弓形} = \frac{1}{2} × \frac{2\pi}{3} × 2 - \frac{1}{2} × 2^{2} × \sin\frac{\pi}{3} = (\frac{2\pi}{3} - \sqrt{3}) cm^{2}$。
(3)设弓形面积为$S_{弓形}$,由题意知$l = \frac{2\pi}{3} cm$,所以$S_{弓形} = \frac{1}{2} × \frac{2\pi}{3} × 2 - \frac{1}{2} × 2^{2} × \sin\frac{\pi}{3} = (\frac{2\pi}{3} - \sqrt{3}) cm^{2}$。
对点练 1 (1)(2025·浙江杭州模拟)半径为 $2$ 的圆上长度为 $4$ 的圆弧所对的圆心角是(
A.$1$
B.$2$
C.$4$
D.$8$
B
)A.$1$
B.$2$
C.$4$
D.$8$
答案:
(1)B
(1)设圆弧所对的圆心角为α,因为半径为2的圆上圆弧长度为4,可得$\alpha × 2 = 4$,所以$\alpha = 2$,故选B。
(1)B
(1)设圆弧所对的圆心角为α,因为半径为2的圆上圆弧长度为4,可得$\alpha × 2 = 4$,所以$\alpha = 2$,故选B。
查看更多完整答案,请扫码查看


