《2026年学易优同步学案导学高中数学选择性必修第一册人教版》

一、两圆位置关系的判断
[梳理导学]
1. 代数法:设两圆的一般方程为
$C_1:x^2+y^2+D_1x+E_1y+F_1=0$($D_1^2+E_1^2-4F_1＞0$),
$C_2:x^2+y^2+D_2x+E_2y+F_2=0$($D_2^2+E_2^2-4F_2＞0$),
联立方程得$\begin{cases}x^2+y^2+D_1x+E_1y+F_1=0,\\x^2+y^2+D_2x+E_2y+F_2=0,\end{cases}$
则方程组解的个数与两圆的位置关系如下：

答案： 1.2　1　0

2. 几何法:若两圆的半径分别为$r_1,r_2$,两圆连心线的长为$d$,则两圆的位置关系如下：

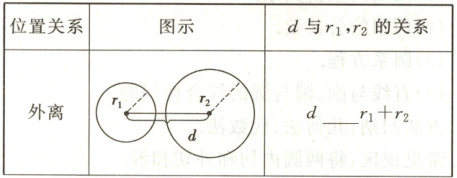
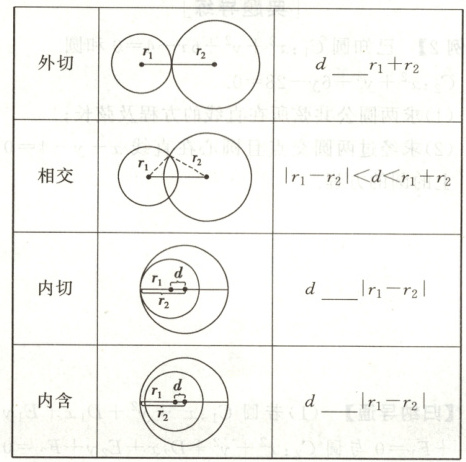
答案： 2.＞　=　=　＜

【例1】 已知圆$C_1:x^2+y^2-2ax-2y+a^2-15=0$($a＞0$),圆$C_2:x^2+y^2-4ax-2y+4a^2=0$($a＞0$).试求$a$为何值时,两圆$C_1,C_2$的位置关系为:
(1) 相切; (2) 相交; (3) 外离; (4) 内含.

答案： 【例1】　[解]　圆$C_1$，$C_2$的方程，经配方后可得
$C_1:(x-a)^2+(y-1)^2=16$
$C_2:(x-2a)^2+(y-1)^2=1$
$\therefore$圆心$C_1(a,1),C_2(2a,1)$，半径$r_1=4,r_2=1$.
$\therefore|C_1C_2|=\sqrt{(a-2a)^2+(1-1)^2}=a$.
(1)当$|C_1C_2|=r_1+r_2=5$，即$a=5$时，两圆外切；
当$|C_1C_2|=r_1-r_2=3$，即$a=3$时，两圆内切.
(2)当$3＜|C_1C_2|＜5$，即$3＜a＜5$时，两圆相交.
(3)当$|C_1C_2|＞5$，即$a＞5$时，两圆外离.
(4)当$|C_1C_2|＜3$，即$0＜a＜3$时，两圆内含.