2026年学易优同步学案导学高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优同步学案导学高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
2. (1) 某考点配备的信号检测设备的监测范围是半径为$ 100 $米的圆形区域,一名工作人员持手机以每分钟$ 50 $米的速度从设备正东方向$ 50\sqrt{6} $米的$ A $处出发,沿西北方向走向位于设备正北方向的$ B $处,则这名工作人员被持续监测的时长为(
A.$ 1 $分钟
B.$ \frac{3}{2} $分钟
C.$ 2 $分钟
D.$ \frac{5}{2} $分钟
C
)A.$ 1 $分钟
B.$ \frac{3}{2} $分钟
C.$ 2 $分钟
D.$ \frac{5}{2} $分钟
答案:
2.
(1)C 以设备的位置为坐标原点O,其正东方向为x轴正方向,正北方向为y轴正方向建立平面直角坐标系Oxy,如图所示,则A(50√6,0),B(0,50√6),可得lAB:x + y = 50√6,圆O:x²+y²=10000。记从N处开始被监测,到M处监测结束,因为O到lAB的距离为|OO'| = $\frac{\vert-50\sqrt{6}\vert}{\sqrt{1² + 1²}}=50\sqrt{3}$(米)。

所以|MN| = 2√(MO² - OO'²)=100(米),故监测时长为$\frac{100}{50}=2$(分钟)。
2.
(1)C 以设备的位置为坐标原点O,其正东方向为x轴正方向,正北方向为y轴正方向建立平面直角坐标系Oxy,如图所示,则A(50√6,0),B(0,50√6),可得lAB:x + y = 50√6,圆O:x²+y²=10000。记从N处开始被监测,到M处监测结束,因为O到lAB的距离为|OO'| = $\frac{\vert-50\sqrt{6}\vert}{\sqrt{1² + 1²}}=50\sqrt{3}$(米)。

所以|MN| = 2√(MO² - OO'²)=100(米),故监测时长为$\frac{100}{50}=2$(分钟)。
(2) 如图是某主题公园的部分景观平面示意图,圆形池塘以$ O $为圆心,以$ 45\sqrt{2} \ m $为半径,$ B $为公园入口,道路$ AB $为东西方向,道路$ AC $经过点$ O $且向正北方向延伸,$ OA = 10 \ m $,$ AB = 100 \ m $,现计划从$ B $处起修一条新路与道路$ AC $相连,且新路在池塘的外围,假设路宽忽略不计,则新路的最小长度为(单位:$ m $)(

A.$ 100\sqrt{2} $
B.$ 100\sqrt{3} $
C.$ 150\sqrt{2} $
D.$ 150\sqrt{3} $
A
)
A.$ 100\sqrt{2} $
B.$ 100\sqrt{3} $
C.$ 150\sqrt{2} $
D.$ 150\sqrt{3} $
答案:
(2)A 以A为坐标原点建立平面直角坐标系(图略),设修建的新路所在直线方程为kx - y + 100k = 0(k>0),则当该直线与圆O相切时,小路长度最小,此时$\frac{\vert100k - 10\vert}{\sqrt{k² + 1}}=45\sqrt{2}$,解得k = 1,此时求得小路长度为100√2m。
(2)A 以A为坐标原点建立平面直角坐标系(图略),设修建的新路所在直线方程为kx - y + 100k = 0(k>0),则当该直线与圆O相切时,小路长度最小,此时$\frac{\vert100k - 10\vert}{\sqrt{k² + 1}}=45\sqrt{2}$,解得k = 1,此时求得小路长度为100√2m。
1. 如图,圆弧形拱桥的跨度$ |AB| = 12 $米,拱高$ |CD| = 4 $米,则拱桥的直径为(
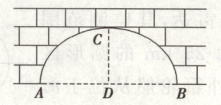
A.$ 15 $米
B.$ 13 $米
C.$ 9 $米
D.$ 6.5 $米
B
)
A.$ 15 $米
B.$ 13 $米
C.$ 9 $米
D.$ 6.5 $米
答案:
1.B 如图,设圆心为O,半径为r,则由勾股定理得|OB|² = |OD|² + |BD|²。
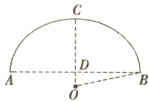
即r²=(r - 4)²+6²,解得r = $\frac{13}{2}$,所以拱桥的直径为13米。
1.B 如图,设圆心为O,半径为r,则由勾股定理得|OB|² = |OD|² + |BD|²。

即r²=(r - 4)²+6²,解得r = $\frac{13}{2}$,所以拱桥的直径为13米。
2. 一艘科考船在点$ O $处监测到北偏东$ 30° $方向$ 40 $海里处有一个小岛$ A $,距离小岛$ 10 $海里范围内可能存在暗礁.若以点$ O $为原点,正东、正北方向分别为$ x $轴、$ y $轴正方向建立平面直角坐标系,则暗礁所在区域边界的方程为(

A.$ (x + 20)^2 + (y - 20\sqrt{3})^2 = 100 $
B.$ (x - 20)^2 + (y + 20\sqrt{3})^2 = 100 $
C.$ (x + 20)^2 + (y + 20\sqrt{3})^2 = 100 $
D.$ (x - 20)^2 + (y - 20\sqrt{3})^2 = 100 $
D
)
A.$ (x + 20)^2 + (y - 20\sqrt{3})^2 = 100 $
B.$ (x - 20)^2 + (y + 20\sqrt{3})^2 = 100 $
C.$ (x + 20)^2 + (y + 20\sqrt{3})^2 = 100 $
D.$ (x - 20)^2 + (y - 20\sqrt{3})^2 = 100 $
答案:
2.D 易得暗礁所在区域边界为一个圆,过A作y轴的垂线,垂足为B(图略),则∠AOB = 30°,
∵|OA| = 40,
∴|AB| = 20,|OB| = √(40² - 20²)=20√3,
∴暗礁所在区域边界方程为(x - 20)²+(y - 20√3)² = 100。
∵|OA| = 40,
∴|AB| = 20,|OB| = √(40² - 20²)=20√3,
∴暗礁所在区域边界方程为(x - 20)²+(y - 20√3)² = 100。
3. 设某村庄外围成圆形,其所在曲线的方程可用$ (x - 2)^2 + (y + 3)^2 = 4 $表示,村外一小路方程可用$ x - y + 2 = 0 $表示,则从村庄外围到小路的最短距离是
$\frac{7\sqrt{2}}{2}-2$
.
答案:
3. 解析:从村庄外围到小路的最短距离为圆心$(2,-3)$到直线$x - y + 2 = 0$的距离减去圆的半径$2$,
即$\frac{|2 + 3 + 2|}{\sqrt{1^{2} + (-1)^{2}}} - 2 = \frac{7\sqrt{2}}{2} - 2$。
答案:$\frac{7\sqrt{2}}{2} - 2$
即$\frac{|2 + 3 + 2|}{\sqrt{1^{2} + (-1)^{2}}} - 2 = \frac{7\sqrt{2}}{2} - 2$。
答案:$\frac{7\sqrt{2}}{2} - 2$
4. 台风中心从$ A $地以$ 20 \ km/h $的速度向东北方向移动,离台风中心$ 30 \ km $内的地区为危险区,城市$ B $在$ A $地正东$ 40 \ km $处,则城市$ B $处于危险区的时间为$ $
1
$ \ h $.
答案:
4. 解析:如图,以 A 地为坐标原点,AB 所在直线为 x 轴,建立平面直角坐标系,
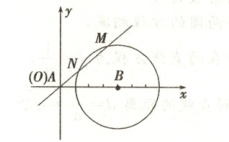
则台风中心经过以$B(40,0)$为圆心,$30$为半径的圆内时城市$B$处于危险区,即$B$处于危险区时,台风中心在线段$MN$上,由题意知,台风路径用方程表示为$y = x$,则圆心$B(40,0)$到直线$y = x$的距离$d = \frac{|40 - 0|}{\sqrt{2}} = 20\sqrt{2}$,可求得$|MN| = 2\sqrt{30^{2} - (20\sqrt{2})^{2}} = 20$,所以城市$B$处于危险区的时间为$1h$。
答案:$1$
4. 解析:如图,以 A 地为坐标原点,AB 所在直线为 x 轴,建立平面直角坐标系,

则台风中心经过以$B(40,0)$为圆心,$30$为半径的圆内时城市$B$处于危险区,即$B$处于危险区时,台风中心在线段$MN$上,由题意知,台风路径用方程表示为$y = x$,则圆心$B(40,0)$到直线$y = x$的距离$d = \frac{|40 - 0|}{\sqrt{2}} = 20\sqrt{2}$,可求得$|MN| = 2\sqrt{30^{2} - (20\sqrt{2})^{2}} = 20$,所以城市$B$处于危险区的时间为$1h$。
答案:$1$
查看更多完整答案,请扫码查看


