2026年学易优同步学案导学高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优同步学案导学高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
2. (1) 若直线的倾斜角为$120^{\circ}$,则直线的斜率_x.(2) 若过点$P(-2,m)$,$Q(m,4)$的直线的斜率为$1$,则$m$的值为
(3) 经过$M(0,3)$,$N(-1,0)$两点的直线的方向向量为$(1,k)$,求$k$的值.
1
.(3) 经过$M(0,3)$,$N(-1,0)$两点的直线的方向向量为$(1,k)$,求$k$的值.
答案:
解析:
(2)由斜率公式$k=\frac{4−m}{m+2}=1,$得m=1.
答案:$(1)−\sqrt{3} (2)1$
(3)解:直线MN的斜率$k_{MN}=\frac{3−0}{0−(−1)}=3,$
∵直线MN的方向向量为(1,k),
∴k=3.
(2)由斜率公式$k=\frac{4−m}{m+2}=1,$得m=1.
答案:$(1)−\sqrt{3} (2)1$
(3)解:直线MN的斜率$k_{MN}=\frac{3−0}{0−(−1)}=3,$
∵直线MN的方向向量为(1,k),
∴k=3.
三、倾斜角和斜率的应用
[探究导思]
问题4 当直线的倾斜角由$0^{\circ}$逐渐增大到$180^{\circ}$,其斜率如何变化?
[探究导思]
问题4 当直线的倾斜角由$0^{\circ}$逐渐增大到$180^{\circ}$,其斜率如何变化?
答案:
探究导思
问题4 提示 当倾斜角为锐角时,斜率为正,而且斜率随着倾斜角的增大而增大;当倾斜角为钝角时,斜率为负,而且斜率随着倾斜角的增大而增大.
问题4 提示 当倾斜角为锐角时,斜率为正,而且斜率随着倾斜角的增大而增大;当倾斜角为钝角时,斜率为负,而且斜率随着倾斜角的增大而增大.
[梳理导学]
1. 设直线的倾斜角为$\alpha$,斜率为$k$.
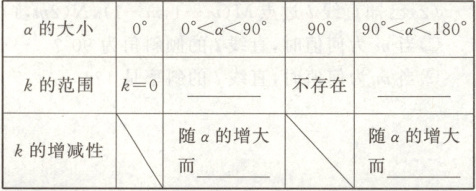
1. 设直线的倾斜角为$\alpha$,斜率为$k$.

答案:
$k>0$;$k<0$;增大;增大
2. 下面特殊角的正切值要熟记:
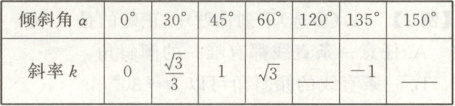

答案:
-√3;-√3/3
【例3】 已知两点$A(-3,4)$,$B(3,2)$,过点$P(1,0)$的直线$l$与线段$AB$有公共点.
(1) 求直线$l$的斜率$k$的取值范围;
(2) 求直线$l$的倾斜角$\alpha$的取值范围.
(1) 求直线$l$的斜率$k$的取值范围;
(2) 求直线$l$的倾斜角$\alpha$的取值范围.
答案:
[例3] [解] 如图,由题意可知$k_{PA}=\frac{4−0}{−3−1}=−1,$$k_{PB}=\frac{2−0}{3−1}=1,$
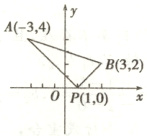
(1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是(−∞,−1]∪[1,+∞).
(2)由题意可知直线l的倾斜角介于直线PB与PA的倾斜角之间,又PB的倾斜角是45°,PA的倾斜角是135°,所以α的取值范围是45°≤α≤135°.
[例3] [解] 如图,由题意可知$k_{PA}=\frac{4−0}{−3−1}=−1,$$k_{PB}=\frac{2−0}{3−1}=1,$

(1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是(−∞,−1]∪[1,+∞).
(2)由题意可知直线l的倾斜角介于直线PB与PA的倾斜角之间,又PB的倾斜角是45°,PA的倾斜角是135°,所以α的取值范围是45°≤α≤135°.
3. 已知点$P(-1,-1)$,另有两点$A(1,0)$,$B(0,1)$,若过点$P$的直线$l$与线段$AB$有交点,则直线$l$的斜率取值范围_x.
答案:
3. 解析:因为A(1,0),B(0,1),又过点P的直线l与线段AB有交点,所以直线l的斜率的取值范围为$[\frac{1}{2},2].$
答案:$[\frac{1}{2},2]$
答案:$[\frac{1}{2},2]$
1. (多选)下列说法正确的是 (
A.若$\alpha$是直线$l$的倾斜角,则$0^{\circ}\leqslant\alpha\lt180^{\circ}$
B.若$k$是直线的斜率,则$k\in\mathbf{R}$
C.任一条直线都有倾斜角,但不一定有斜率
D.任一条直线都有斜率,但不一定有倾斜角
ABC
)A.若$\alpha$是直线$l$的倾斜角,则$0^{\circ}\leqslant\alpha\lt180^{\circ}$
B.若$k$是直线的斜率,则$k\in\mathbf{R}$
C.任一条直线都有倾斜角,但不一定有斜率
D.任一条直线都有斜率,但不一定有倾斜角
答案:
1.ABC 由直线的倾斜角和斜率的定义知,A、B、C正确,D错误. 故选ABC.
2. 若经过$A(m,3)$,$B(1,2)$两点的直线的倾斜角为$45^{\circ}$,则$m$等于 (
A.$2$
B.$1$
C.$-1$
D.$-2$
A
)A.$2$
B.$1$
C.$-1$
D.$-2$
答案:
2.A 由题意知,$tan 45°=\frac{2−3}{1−m}=1,$得m=2.
3. 过点$A(-\sqrt{3},\sqrt{2})$与点$B(-\sqrt{2},\sqrt{3})$的直线的倾斜角为 (
A.$45^{\circ}$
B.$135^{\circ}$
C.$45^{\circ}$或$135^{\circ}$
D.$60^{\circ}$
A
)A.$45^{\circ}$
B.$135^{\circ}$
C.$45^{\circ}$或$135^{\circ}$
D.$60^{\circ}$
答案:
$3.A k_{AB}=\frac{\sqrt{3}−\sqrt{2}}{−\sqrt{2}−(−\sqrt{3})}=\frac{\sqrt{3}−\sqrt{2}}{\sqrt{3}−\sqrt{2}}=1,$故直线的倾斜角为45°.
4. 经过$A(m,3)$,$B(1,2)$两点的直线的倾斜角$\alpha$的取值范围是
0°<α≤90°
.(其中$m\geqslant1$)
答案:
4. 解析:当m=1时,倾斜角α=90°;当m>1时,$tan α=\frac{3−2}{m−1}>0,$
∴0°<α<90°. 故0°<α≤90°.
答案:0°<α≤90°
∴0°<α<90°. 故0°<α≤90°.
答案:0°<α≤90°
查看更多完整答案,请扫码查看


