2026年学易优同步学案导学高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优同步学案导学高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
一、点到直线的距离
[探究导思]
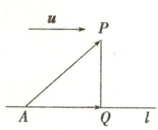
问题1 如图,已知直线$ l $的单位方向向量为$ \boldsymbol{u} $,$ A $是直线$ l $上的定点,$ P $是直线$ l $外一点.如何利用这些条件求点$ P $到直线$ l $的距离?
问题2 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
[探究导思]

问题1 如图,已知直线$ l $的单位方向向量为$ \boldsymbol{u} $,$ A $是直线$ l $上的定点,$ P $是直线$ l $外一点.如何利用这些条件求点$ P $到直线$ l $的距离?
问题2 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
答案:
问题1 提示 设$\overrightarrow{AP}=\boldsymbol{a}$,则向量$\overrightarrow{AP}$在直线$l$上的投影向量$\overrightarrow{AQ}=(\boldsymbol{a}·\boldsymbol{u})\boldsymbol{u}$.在$Rt\triangle APQ$中,由勾股定理,得点$P$到直线$l$的距离为$PQ=\sqrt{|\overrightarrow{AP}|^{2}-|\overrightarrow{AQ}|^{2}}=\sqrt{\boldsymbol{a}^{2}-(\boldsymbol{a}·\boldsymbol{u})^{2}}$.
问题2 提示 在其中一条直线上取定一点,则该点到另一条直线的距离即为两条平行直线之间的距离.
问题2 提示 在其中一条直线上取定一点,则该点到另一条直线的距离即为两条平行直线之间的距离.
【例1】 在长方体$ OABC - O_1A_1B_1C_1 $中,$ OA = 2 $,$ AB = 3 $,$ AA_1 = 2 $,求$ O_1 $到直线$ AC $的距离.
答案:
【例1】 [解] 方法一:连接$AO_1$,建立如图所示的空间直角坐标系,
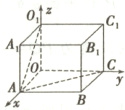
则$A(2,0,0)$,$O_1(0,0,2)$,$C(0,3,0)$,
$\therefore\overrightarrow{AO_1}=(-2,0,2)$,$\overrightarrow{AC}=(-2,3,0)$,
$\therefore\overrightarrow{AO_1}·\overrightarrow{AC}=(-2,0,2)·(-2,3,0)=4$,
取$\boldsymbol{a}=\overrightarrow{AO_1}=(-2,0,2)$,
$\boldsymbol{u}=\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}=\left(\frac{-2}{\sqrt{13}},\frac{3}{\sqrt{13}},0\right)$,
$\therefore\boldsymbol{a}·\boldsymbol{u}=\frac{4}{\sqrt{13}}$,
$\therefore O_1$到直线$AC$的距离
$d=\sqrt{\boldsymbol{a}^{2}-(\boldsymbol{a}·\boldsymbol{u})^{2}}=\frac{2\sqrt{286}}{13}$.
方法二:建立如图所示的空间直角坐标系,则$A(2,0,0)$,$O_1(0,0,2)$,$C(0,3,0)$,过$O_1$作$O_1D\perp AC$于点$D$,设$D(x,y,0)$,则$\overrightarrow{O_1D}=(x,y,-2)$,$\overrightarrow{AD}=(x-2,y,0)$.
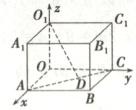
$\because\overrightarrow{AC}=(-2,3,0)$,$\overrightarrow{O_1D}\perp\overrightarrow{AC}$,$\overrightarrow{AD}//\overrightarrow{AC}$,
$\therefore\begin{cases}-2x+3y=0,\frac{x-2}{-2}=\frac{y}{3},\end{cases}$解得$\begin{cases}x=\frac{18}{13},\\y=\frac{12}{13}.\end{cases}$
$\therefore D\left(\frac{18}{13},\frac{12}{13},0\right)$,
$\therefore|\overrightarrow{O_1D}|=\sqrt{\left(\frac{18}{13}\right)^{2}+\left(\frac{12}{13}\right)^{2}+(-2)^{2}}=\frac{2\sqrt{286}}{13}$.
即$O_1$到直线$AC$的距离为$\frac{2\sqrt{286}}{13}$.
【例1】 [解] 方法一:连接$AO_1$,建立如图所示的空间直角坐标系,

则$A(2,0,0)$,$O_1(0,0,2)$,$C(0,3,0)$,
$\therefore\overrightarrow{AO_1}=(-2,0,2)$,$\overrightarrow{AC}=(-2,3,0)$,
$\therefore\overrightarrow{AO_1}·\overrightarrow{AC}=(-2,0,2)·(-2,3,0)=4$,
取$\boldsymbol{a}=\overrightarrow{AO_1}=(-2,0,2)$,
$\boldsymbol{u}=\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}=\left(\frac{-2}{\sqrt{13}},\frac{3}{\sqrt{13}},0\right)$,
$\therefore\boldsymbol{a}·\boldsymbol{u}=\frac{4}{\sqrt{13}}$,
$\therefore O_1$到直线$AC$的距离
$d=\sqrt{\boldsymbol{a}^{2}-(\boldsymbol{a}·\boldsymbol{u})^{2}}=\frac{2\sqrt{286}}{13}$.
方法二:建立如图所示的空间直角坐标系,则$A(2,0,0)$,$O_1(0,0,2)$,$C(0,3,0)$,过$O_1$作$O_1D\perp AC$于点$D$,设$D(x,y,0)$,则$\overrightarrow{O_1D}=(x,y,-2)$,$\overrightarrow{AD}=(x-2,y,0)$.

$\because\overrightarrow{AC}=(-2,3,0)$,$\overrightarrow{O_1D}\perp\overrightarrow{AC}$,$\overrightarrow{AD}//\overrightarrow{AC}$,
$\therefore\begin{cases}-2x+3y=0,\frac{x-2}{-2}=\frac{y}{3},\end{cases}$解得$\begin{cases}x=\frac{18}{13},\\y=\frac{12}{13}.\end{cases}$
$\therefore D\left(\frac{18}{13},\frac{12}{13},0\right)$,
$\therefore|\overrightarrow{O_1D}|=\sqrt{\left(\frac{18}{13}\right)^{2}+\left(\frac{12}{13}\right)^{2}+(-2)^{2}}=\frac{2\sqrt{286}}{13}$.
即$O_1$到直线$AC$的距离为$\frac{2\sqrt{286}}{13}$.
1. 如图,$ P $为矩形$ ABCD $所在平面外一点,$ PA \perp $平面$ ABCD $,若已知$ AB = 3 $,$ AD = 4 $,$ PA = 1 $,求点$ P $到$ BD $的距离.
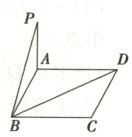

答案:
1.解:如图,分别以$\overrightarrow{AB}$,$\overrightarrow{AD}$,$\overrightarrow{AP}$所在直线为$x$,$y$,$z$轴正方向建立空间直角坐标系,

则$P(0,0,1)$,$B(3,0,0)$,$D(0,4,0)$,
所以$\overrightarrow{PB}=(3,0,-1)$,
$\overrightarrow{BD}=(-3,4,0)$,
取$\boldsymbol{a}=\overrightarrow{PB}=(3,0,-1)$,$\boldsymbol{u}=\frac{\overrightarrow{BD}}{|\overrightarrow{BD}|}=\left(-\frac{3}{5},\frac{4}{5},0\right)$,
则$\boldsymbol{a}^{2}=10$,$\boldsymbol{a}·\boldsymbol{u}=-\frac{9}{5}$,
所以点$P$到$BD$的距离为$\sqrt{\boldsymbol{a}^{2}-(\boldsymbol{a}·\boldsymbol{u})^{2}}=\sqrt{10-\frac{81}{25}}=\frac{13}{5}$.
1.解:如图,分别以$\overrightarrow{AB}$,$\overrightarrow{AD}$,$\overrightarrow{AP}$所在直线为$x$,$y$,$z$轴正方向建立空间直角坐标系,

则$P(0,0,1)$,$B(3,0,0)$,$D(0,4,0)$,
所以$\overrightarrow{PB}=(3,0,-1)$,
$\overrightarrow{BD}=(-3,4,0)$,
取$\boldsymbol{a}=\overrightarrow{PB}=(3,0,-1)$,$\boldsymbol{u}=\frac{\overrightarrow{BD}}{|\overrightarrow{BD}|}=\left(-\frac{3}{5},\frac{4}{5},0\right)$,
则$\boldsymbol{a}^{2}=10$,$\boldsymbol{a}·\boldsymbol{u}=-\frac{9}{5}$,
所以点$P$到$BD$的距离为$\sqrt{\boldsymbol{a}^{2}-(\boldsymbol{a}·\boldsymbol{u})^{2}}=\sqrt{10-\frac{81}{25}}=\frac{13}{5}$.
查看更多完整答案,请扫码查看


