2025年同步练习册人民教育出版社高中化学选择性必修第一册人教版B山东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年同步练习册人民教育出版社高中化学选择性必修第一册人教版B山东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
7. (双选)在$25^{\circ}C$时,密闭容器中$X$、$Y$、$Z$三种气体的初始浓度和平衡浓度如表所示。
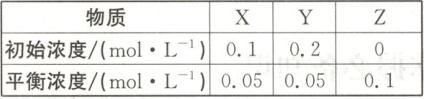
下列说法错误的是(
A.反应达到平衡时,$X$的转化率为$60\%$
B.反应可表示为$X(g)+3Y(g)⇌ 2Z(g)$,其平衡常数为$1600$
C.改变温度可以改变此反应的平衡常数
D.反应前后压强之比为$2:3$

下列说法错误的是(
AD
)。A.反应达到平衡时,$X$的转化率为$60\%$
B.反应可表示为$X(g)+3Y(g)⇌ 2Z(g)$,其平衡常数为$1600$
C.改变温度可以改变此反应的平衡常数
D.反应前后压强之比为$2:3$
答案:
AD 解析X、Y、Z的浓度变化量分别为$0.05 mol·L^{-1}、$$0.15 mol·L^{-1}、$$0.1 mol·L^{-1},$且X、Y的浓度减小,Z的浓度增大,所以该反应的化学方程式为X(g)+3Y(g)⇌2Z(g),平衡常数$K=\frac{0.1^2}{0.05×0.05^3}=1600,$B项正确;X的转化率为$\frac{0.05 mol·L^{-1}}{0.1 mol·L^{-1}}×100%=50%,$A项错误;平衡常数受温度的影响,改变温度能改变该反应的平衡常数,C项正确;反应前后压强之比为$\frac{0.1+0.2}{0.05+0.05+0.1}=3:2,$D项错误。
8. 工业上以$CH_{4}$为原料制备$H_{2}$的原理为$CH_{4}(g)+H_{2}O(g)⇌ CO(g)+3H_{2}(g)$ $\Delta H>0$。在一定条件下,向$a$、$b$两个恒温的密闭容器中均通入$1.1\ mol\ CH_{4}(g)$和$1.1\ mol\ H_{2}O(g)$,测得两容器中$CO$的物质的量随时间的变化曲线分别为$a$和$b$。已知容器$a$、$b$的容积均为$10\ L$,容器$a$的温度为$T_{a}$,容器$b$的温度为$T_{b}$,下列说法不正确的是(
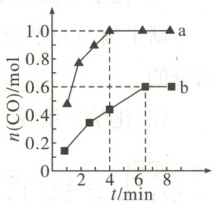
A.容器$a$中$CH_{4}$从反应开始到恰好平衡时的平均反应速率为$0.025\ mol· L^{-1}· min^{-1}$
B.$a$、$b$两容器的温度可能相同
C.在达到平衡前,容器$a$中的气体压强逐渐增大
D.该反应在$T_{a}$温度下的平衡常数为$27$
B
)。
A.容器$a$中$CH_{4}$从反应开始到恰好平衡时的平均反应速率为$0.025\ mol· L^{-1}· min^{-1}$
B.$a$、$b$两容器的温度可能相同
C.在达到平衡前,容器$a$中的气体压强逐渐增大
D.该反应在$T_{a}$温度下的平衡常数为$27$
答案:
B 解析根据题意,列出容器a中反应的三段式,
$CH_4(g)+H_2O(g)⇌CO(g)+3H_2(g)$
起始$/(mol·L^{-1}) 0.11 0.11 0 0$
变化$/(mol·L^{-1}) 0.1 0.1 0.1 0.3$
平衡$/(mol·L^{-1}) 0.01 0.01 0.1 0.3$
容器a中$CH_4$从反应开始到恰好平衡时的平均反应速率为$v(CH_4)=\frac{0.1 mol·L^{-1}}{4 min}=0.025 mol·L^{-1}·min^{-1},$A项正确;由图可知,容器a中的反应先达到平衡状态,因此T_a>T_b,B项错误;因为该反应条件为恒温恒容,反应后气体的物质的量增大,所以在达到平衡前,容器a中的气体压强逐渐增大,C项正确;该反应在T_a温度下的平衡常数为$\frac{c(CO)·c^3(H_2)}{c(CH_4)·c(H_2O)}=\frac{0.1×0.3^3}{0.01×0.01}=27,$D项正确。
$CH_4(g)+H_2O(g)⇌CO(g)+3H_2(g)$
起始$/(mol·L^{-1}) 0.11 0.11 0 0$
变化$/(mol·L^{-1}) 0.1 0.1 0.1 0.3$
平衡$/(mol·L^{-1}) 0.01 0.01 0.1 0.3$
容器a中$CH_4$从反应开始到恰好平衡时的平均反应速率为$v(CH_4)=\frac{0.1 mol·L^{-1}}{4 min}=0.025 mol·L^{-1}·min^{-1},$A项正确;由图可知,容器a中的反应先达到平衡状态,因此T_a>T_b,B项错误;因为该反应条件为恒温恒容,反应后气体的物质的量增大,所以在达到平衡前,容器a中的气体压强逐渐增大,C项正确;该反应在T_a温度下的平衡常数为$\frac{c(CO)·c^3(H_2)}{c(CH_4)·c(H_2O)}=\frac{0.1×0.3^3}{0.01×0.01}=27,$D项正确。
9. 一定条件下,$0.3\ mol\ X(g)$与$0.3\ mol\ Y(g)$在容积固定的密闭容器中发生反应:$X(g)+3Y(g)⇌ 2Z(g)$ $\Delta H = -a\ kJ· mol^{-1}$,下列说法正确的是(
A.反应一段时间后,$X$与$Y$的物质的量之比仍为$1:1$
B.达到平衡时,反应放出$0.1a\ kJ$的热量
C.达到平衡后,若向平衡体系中充入稀有气体,$Z$的正反应速率将不发生变化
D.$X$的体积分数保持不变,说明反应已达到平衡
C
)。A.反应一段时间后,$X$与$Y$的物质的量之比仍为$1:1$
B.达到平衡时,反应放出$0.1a\ kJ$的热量
C.达到平衡后,若向平衡体系中充入稀有气体,$Z$的正反应速率将不发生变化
D.$X$的体积分数保持不变,说明反应已达到平衡
答案:
C 解析根据题意列三段式:
X(g) + 3Y(g)⇌2Z(g)
起始/mol 0.3 0.3 0
变化/mol x 3x 2x
某时刻/mol 0.3-x 0.3-3x 2x
X的体积分数为$\frac{0.3-x}{0.6-2x}×100%=50%,$
X的体积分数始终保持不变,不能说明反应已达到平衡,D项错误。
X(g) + 3Y(g)⇌2Z(g)
起始/mol 0.3 0.3 0
变化/mol x 3x 2x
某时刻/mol 0.3-x 0.3-3x 2x
X的体积分数为$\frac{0.3-x}{0.6-2x}×100%=50%,$
X的体积分数始终保持不变,不能说明反应已达到平衡,D项错误。
10. 在$1.0\ L$密闭容器中放入$0.10\ mol\ A(g)$,在一定温度下进行如下反应:$A(g)⇌ B(g)+C(g)$ $\Delta H=+85.1\ kJ· mol^{-1}$。
反应时间($t$)与容器内气体总压强($p$)的数据见下表。
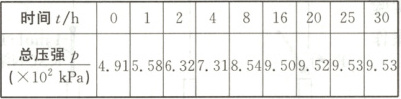
|总压强$p(× 10^{2}kPa)$|4.91|5.58|6.32|7.31|8.54|9.50|9.52|9.53|9.53|
(1)一定处于平衡状态的时间段是_,由总压强$p$和起始压强$p_{0}$计算反应物$A$的转化率的表达式为_,计算平衡时$A$的转化率为_(保留$1$位小数,下同),反应的平衡常数$K=$__。
(2)①由总压强$p$和起始压强$p_{0}$表示反应体系的总物质的量$n_{总}$和反应物$A$的物质的量$n(A)$,$n_{总}=$
②下表为反应物$A$的浓度与反应时间的数据。
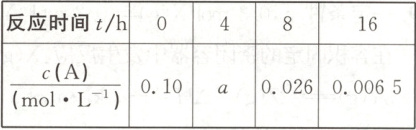
$a=$
分析该反应中反应物的浓度$c(A)$变化与时间间隔($\Delta t$)的规律,得出的结论是_,由此规律推出反应在$12\ h$时反应物的浓度$c(A)$约为_ $mol· L^{-1}$。
反应时间($t$)与容器内气体总压强($p$)的数据见下表。

|总压强$p(× 10^{2}kPa)$|4.91|5.58|6.32|7.31|8.54|9.50|9.52|9.53|9.53|
(1)一定处于平衡状态的时间段是_,由总压强$p$和起始压强$p_{0}$计算反应物$A$的转化率的表达式为_,计算平衡时$A$的转化率为_(保留$1$位小数,下同),反应的平衡常数$K=$__。
(2)①由总压强$p$和起始压强$p_{0}$表示反应体系的总物质的量$n_{总}$和反应物$A$的物质的量$n(A)$,$n_{总}=$
0.10×\frac{p}{p_0}
$mol$,$n(A)=$0.10×(2-\frac{p}{p_0})
$mol$。②下表为反应物$A$的浓度与反应时间的数据。

$a=$
0.051
。分析该反应中反应物的浓度$c(A)$变化与时间间隔($\Delta t$)的规律,得出的结论是_,由此规律推出反应在$12\ h$时反应物的浓度$c(A)$约为_ $mol· L^{-1}$。
答案:
$(1)25~30 h (\frac{p}{p_0}-1)×100% 94.1%$
$1.5 (2)①0.10×\frac{p}{p_0} 0.10×(2-\frac{p}{p_0}) ②0.051 $达到平衡前每间隔4 h,c(A)约减少一半 0.013
解析
(1)25~30 h一定处于平衡状态,在温度、容积一定的条件下,气体的压强之比等于其物质的量(物质的量浓度)之比。对于反应A(g)⇌B(g)+C(g),体系总压强的变化量等于气体A压强的变化量,则$α(A)=\frac{Δn}{n(A)}×100%=\frac{Δp}{p_0}×100%=\frac{p-p_0}{p_0}×100%=(\frac{p}{p_0}-1)×100%。$
$p_0=4.91×10^2 kPa,$平衡时,$p=9.53×10^2 kPa,$
则$α(A)=(\frac{9.53×10^2}{4.91×10^2}-1)×100%≈94.1%。$
A(g)⇌B(g) + C(g)
起始/mol 0.10 0 0
平衡/mol 0.10×5.9% 0.10×94.1% 0.10×94.1%
$K=\frac{0.094 1^2}{0.005 9}≈1.5。$
(2)①恒温恒容下,$\frac{n_0}{n_总}=\frac{p}{p_0},$则n_总$=0.10×\frac{p}{p_0}mol。$
A(g)⇌B(g) + C(g)
起始 0.10 mol 0 0
某时刻 n(A) 0.10 mol—n(A) 0.10 mol—n(A)
n_总=0.20 mol—n(A),则n(A)=0.20 mol—n_总$=0.20 mol—0.10×\frac{p}{p_0}mol=0.10×(2-\frac{p}{p_0})mol。$
②由表中数据可知,4 h时,$p=7.31×10^2 kPa,$则4 h时$n(A)=0.10×(2-\frac{p}{p_0})mol=0.10×(2-\frac{7.31×10^2}{4.91×10^2})mol≈0.051 mol,$故$c(A)=0.051 mol·L^{-1},$即a=0.051。由表中反应物A的浓度变化与时间间隔(Δt)之间的关系可知,达到平衡前每间隔4 h,c(A)约减少一半。
8 h时,$c(A)=0.026 mol·L^{-1},$再经过4 h,即12 h时,反应物的浓度c(A)约为8 h时浓度的一半,即为$0.013 mol·L^{-1}。$
$1.5 (2)①0.10×\frac{p}{p_0} 0.10×(2-\frac{p}{p_0}) ②0.051 $达到平衡前每间隔4 h,c(A)约减少一半 0.013
解析
(1)25~30 h一定处于平衡状态,在温度、容积一定的条件下,气体的压强之比等于其物质的量(物质的量浓度)之比。对于反应A(g)⇌B(g)+C(g),体系总压强的变化量等于气体A压强的变化量,则$α(A)=\frac{Δn}{n(A)}×100%=\frac{Δp}{p_0}×100%=\frac{p-p_0}{p_0}×100%=(\frac{p}{p_0}-1)×100%。$
$p_0=4.91×10^2 kPa,$平衡时,$p=9.53×10^2 kPa,$
则$α(A)=(\frac{9.53×10^2}{4.91×10^2}-1)×100%≈94.1%。$
A(g)⇌B(g) + C(g)
起始/mol 0.10 0 0
平衡/mol 0.10×5.9% 0.10×94.1% 0.10×94.1%
$K=\frac{0.094 1^2}{0.005 9}≈1.5。$
(2)①恒温恒容下,$\frac{n_0}{n_总}=\frac{p}{p_0},$则n_总$=0.10×\frac{p}{p_0}mol。$
A(g)⇌B(g) + C(g)
起始 0.10 mol 0 0
某时刻 n(A) 0.10 mol—n(A) 0.10 mol—n(A)
n_总=0.20 mol—n(A),则n(A)=0.20 mol—n_总$=0.20 mol—0.10×\frac{p}{p_0}mol=0.10×(2-\frac{p}{p_0})mol。$
②由表中数据可知,4 h时,$p=7.31×10^2 kPa,$则4 h时$n(A)=0.10×(2-\frac{p}{p_0})mol=0.10×(2-\frac{7.31×10^2}{4.91×10^2})mol≈0.051 mol,$故$c(A)=0.051 mol·L^{-1},$即a=0.051。由表中反应物A的浓度变化与时间间隔(Δt)之间的关系可知,达到平衡前每间隔4 h,c(A)约减少一半。
8 h时,$c(A)=0.026 mol·L^{-1},$再经过4 h,即12 h时,反应物的浓度c(A)约为8 h时浓度的一半,即为$0.013 mol·L^{-1}。$
查看更多完整答案,请扫码查看


