《2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版》

22. (12分)(锦州期末)
【问题情境】
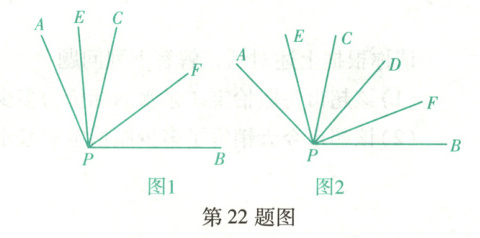
如图1,$ \angle APB = \alpha ( 0 ^ { \circ } ＜ \alpha \leq 180 ^ { \circ } ) $,在$ \angle APB $内部作射线PC(不与PA,PB重合),射线PE,PF分别平分$ \angle APC $和$ \angle BPC $.
【特例感知】
(1)若$ \alpha = 120 ^ { \circ } $,$ \angle APC = 40 ^ { \circ } $,求$ \angle EPF $的度数.
【猜想验证】
(2)猜想$ \angle EPF $与$ \alpha $之间的数量关系,并说明理由.
【拓展延伸】
(3)小张同学由此受到启发,对问题进行了深入思考,提出了如下问题,请你解答.
如图2,$ \angle APB = \alpha ( 0 ^ { \circ } ＜ \alpha \leq 180 ^ { \circ } ) $,在$ \angle APB $内部作$ \angle CPD $(PC,PD不与PA,PB重合),射线PE,PF分别平分$ \angle APC $和$ \angle BPD $.若$ \angle CPD = \beta ( \beta ＜ \alpha ) $,求$ \angle EPF $的度数(用含$ \alpha , \beta $的代数式表示).

答案： 22.解：
(1)
∵α=120°，∠APC=40°，
∴∠BPC=α-∠APC=80°，
∵PE，PF分别平分∠APC和∠BPC，
∴∠EPC= $\frac{1}{2}$∠APC=20°，∠FPC= $\frac{1}{2}$∠BPC=40°，
∴∠EPF=∠EPC+∠FPC=60°.
(2)猜想∠EPF= $\frac{1}{2}$α，理由如下：
∵PE，PF分别平分∠APC和∠BPC，
∴∠EPC= $\frac{1}{2}$∠APC，∠FPC= $\frac{1}{2}$∠BPC，
∴∠EPF=∠EPC+∠FPC= $\frac{1}{2}$(∠APC+∠BPC)= $\frac{1}{2}$∠APB= $\frac{1}{2}$α.
(3)
∵PE，PF分别平分∠APC和∠BPC，
∴∠EPC= $\frac{1}{2}$∠APC，∠FPD= $\frac{1}{2}$∠BPD，
∴∠EPC+∠FPD= $\frac{1}{2}$(∠APC+∠BPD)= $\frac{1}{2}$(∠APB-∠CPD)= $\frac{1}{2}$(α-β)，
∴∠EPF=∠EPC+∠FPD+∠CPD= $\frac{1}{2}$(α-β)+β= $\frac{1}{2}$α+ $\frac{1}{2}$β.