2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23. (13分)
从一个角的顶点出发, 在角的内部引两条射线, 如果这两条射线所成的角等于这个角的一半, 那么这两条射线所成的角叫作这个角的内半角.
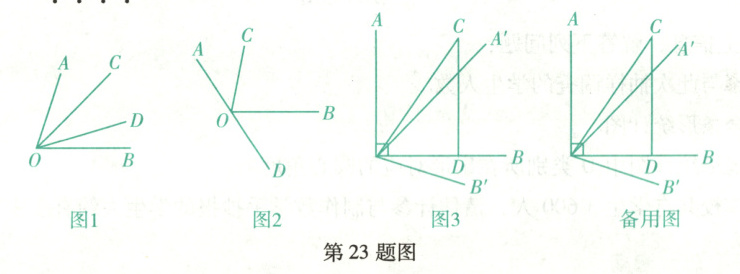
如图1, 若射线 $ OC $, $ OD $ 在 $ \angle AOB $ 的内部, 且 $ \angle COD = \frac{1}{2}\angle AOB $, 则 $ \angle COD $ 是 $ \angle AOB $ 的内半角.
(1)如图1, $ \angle AOB = 70^{\circ} $, $ \angle AOC = 25^{\circ} $. 若 $ \angle COD $ 是 $ \angle AOB $ 的内半角, 求 $ \angle BOD $ 的度数.
(2)如图2, 已知 $ \angle AOB = 120^{\circ} $, 将 $ \angle AOB $ 绕点 $ O $ 按顺时针方向旋转一个角度 $ \alpha(0^{\circ} < \alpha < 120^{\circ}) $ 至 $ \angle COD $. 若 $ \angle COB $ 是 $ \angle AOD $ 的内半角, 求 $ \alpha $ 的值.
(3)如图3, 已知 $ \angle AOB = 90^{\circ} $, 把三角板 $ COD $ 按如图3放置($ \angle COD = 60^{\circ} $), $ OA $, $ OB $ 分别以 $ 15^{\circ}/s $ 和 $ 10^{\circ}/s $ 按顺时针方向转动一周, 当射线 $ OA $, $ OB $, $ OC $, $ OD $ 构成内半角时, 请直
从一个角的顶点出发, 在角的内部引两条射线, 如果这两条射线所成的角等于这个角的一半, 那么这两条射线所成的角叫作这个角的内半角.
如图1, 若射线 $ OC $, $ OD $ 在 $ \angle AOB $ 的内部, 且 $ \angle COD = \frac{1}{2}\angle AOB $, 则 $ \angle COD $ 是 $ \angle AOB $ 的内半角.
(1)如图1, $ \angle AOB = 70^{\circ} $, $ \angle AOC = 25^{\circ} $. 若 $ \angle COD $ 是 $ \angle AOB $ 的内半角, 求 $ \angle BOD $ 的度数.
(2)如图2, 已知 $ \angle AOB = 120^{\circ} $, 将 $ \angle AOB $ 绕点 $ O $ 按顺时针方向旋转一个角度 $ \alpha(0^{\circ} < \alpha < 120^{\circ}) $ 至 $ \angle COD $. 若 $ \angle COB $ 是 $ \angle AOD $ 的内半角, 求 $ \alpha $ 的值.
(3)如图3, 已知 $ \angle AOB = 90^{\circ} $, 把三角板 $ COD $ 按如图3放置($ \angle COD = 60^{\circ} $), $ OA $, $ OB $ 分别以 $ 15^{\circ}/s $ 和 $ 10^{\circ}/s $ 按顺时针方向转动一周, 当射线 $ OA $, $ OB $, $ OC $, $ OD $ 构成内半角时, 请直
接
写
出
$ t $ 的值.
答案:
23.解:
(1)$\because\angle COD$是$\angle AOB$的内半角,$\angle AOB = 70^{\circ}$,$\therefore\angle COD = \frac{1}{2}\angle AOB = 35^{\circ}$,$\therefore\angle BOD = \angle AOB - \angle AOC - \angle COD = 70^{\circ} - 25^{\circ} - 35^{\circ} = 10^{\circ}$。
(2)由旋转的性质知$\angle AOC = \angle BOD = \alpha$,$\angle COD = \angle AOB = 120^{\circ}$,$\therefore\angle AOD = \angle AOC + \angle COD = \alpha + 120^{\circ}$,$\angle COB = \angle AOB - \angle AOC = 120^{\circ} - \alpha$,$\because\angle COB$是$\angle AOD$的内半角,$\therefore\angle AOD = 2\angle COB$,即$\alpha + 120^{\circ} = 2(120^{\circ} - \alpha)$,解得$\alpha = 40^{\circ}$。
(3)分五种情况:①如答图1,当$0 < t < 2$,且$\angle COD$是$\angle AOB$的内半角时,有$90 - 15t + 10t = 60×2$,解得$t = -6$(舍去);②如答图2,当$2 < t < 6$,且$\angle AOD$是$\angle BOC$的内半角时,有$2(90 - 15t) = 60 + 10t$,解得$t = 3$;③如答图3,当$6 < t < 18$,且$\angle AOD$是$\angle BOC$的内半角时,有$2(15t - 90) = 60 + 10t$,解得$t = 12$;④如答图4,当$18 < t\leq24$,且$\angle AOC$是$\angle BOD$的内半角时,有$2(360 - 15t + 90 - 60^{\circ}) = 360 - 10t$,解得$t = 21$;⑤如答图5,当$24 < t < 36$,且$\angle BOC$是$\angle AOD$的内半角时,有$360 - 10t = 90 - 90×\frac{1}{2} - 90 - 60$,解得$t = 34.5$。





综上所述,当$t$的值为3或12或21或34.5时,射线$OA$,$OB$,$OC$,$OD$构成内半角。
23.解:
(1)$\because\angle COD$是$\angle AOB$的内半角,$\angle AOB = 70^{\circ}$,$\therefore\angle COD = \frac{1}{2}\angle AOB = 35^{\circ}$,$\therefore\angle BOD = \angle AOB - \angle AOC - \angle COD = 70^{\circ} - 25^{\circ} - 35^{\circ} = 10^{\circ}$。
(2)由旋转的性质知$\angle AOC = \angle BOD = \alpha$,$\angle COD = \angle AOB = 120^{\circ}$,$\therefore\angle AOD = \angle AOC + \angle COD = \alpha + 120^{\circ}$,$\angle COB = \angle AOB - \angle AOC = 120^{\circ} - \alpha$,$\because\angle COB$是$\angle AOD$的内半角,$\therefore\angle AOD = 2\angle COB$,即$\alpha + 120^{\circ} = 2(120^{\circ} - \alpha)$,解得$\alpha = 40^{\circ}$。
(3)分五种情况:①如答图1,当$0 < t < 2$,且$\angle COD$是$\angle AOB$的内半角时,有$90 - 15t + 10t = 60×2$,解得$t = -6$(舍去);②如答图2,当$2 < t < 6$,且$\angle AOD$是$\angle BOC$的内半角时,有$2(90 - 15t) = 60 + 10t$,解得$t = 3$;③如答图3,当$6 < t < 18$,且$\angle AOD$是$\angle BOC$的内半角时,有$2(15t - 90) = 60 + 10t$,解得$t = 12$;④如答图4,当$18 < t\leq24$,且$\angle AOC$是$\angle BOD$的内半角时,有$2(360 - 15t + 90 - 60^{\circ}) = 360 - 10t$,解得$t = 21$;⑤如答图5,当$24 < t < 36$,且$\angle BOC$是$\angle AOD$的内半角时,有$360 - 10t = 90 - 90×\frac{1}{2} - 90 - 60$,解得$t = 34.5$。





综上所述,当$t$的值为3或12或21或34.5时,射线$OA$,$OB$,$OC$,$OD$构成内半角。
查看更多完整答案,请扫码查看


