2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23.(13分)
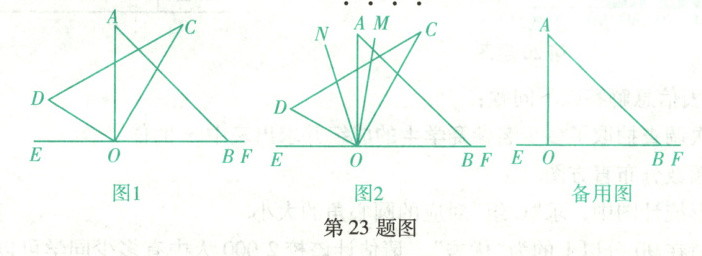
如图,$O$为直线$EF$上一点,将一副直角三角尺的两个直角顶点叠合在$O$处,其中一个直角三角尺的另一顶点落在直线$EF$上的点$B$处.(本题涉及的角均小于或等于$180^{\circ}$)
(1)如图1,若$\angle AOC = 30^{\circ}$,求$\angle DOB$的度数.
(2)将直角三角尺$ODC$从图1的位置绕点$O$按逆时针方向旋转$\alpha(0^{\circ} < \alpha < 90^{\circ})$. 若$\angle AOD = 5\angle AOC$,求$\angle DOB$的度数.
(3)将直角三角尺$ODC$从如图2的位置绕点$O$按逆时针方向旋转一周,射线$ON$在$\angle AOD$内,射线$OM$在$\angle AOC$内,且$\angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,在转动过程中某个位置测得$\angle MON = 63^{\circ}$,请直
如图,$O$为直线$EF$上一点,将一副直角三角尺的两个直角顶点叠合在$O$处,其中一个直角三角尺的另一顶点落在直线$EF$上的点$B$处.(本题涉及的角均小于或等于$180^{\circ}$)
(1)如图1,若$\angle AOC = 30^{\circ}$,求$\angle DOB$的度数.
(2)将直角三角尺$ODC$从图1的位置绕点$O$按逆时针方向旋转$\alpha(0^{\circ} < \alpha < 90^{\circ})$. 若$\angle AOD = 5\angle AOC$,求$\angle DOB$的度数.
(3)将直角三角尺$ODC$从如图2的位置绕点$O$按逆时针方向旋转一周,射线$ON$在$\angle AOD$内,射线$OM$在$\angle AOC$内,且$\angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,在转动过程中某个位置测得$\angle MON = 63^{\circ}$,请直
接
写
出
$n$的值.
答案:
23.解:
(1)由题意得$\angle AOB = \angle COD = 90^{\circ}$,$\because \angle AOC = 30^{\circ}$,$\therefore \angle AOD = \angle COD - \angle AOC = 90^{\circ} - 30^{\circ} = 60^{\circ}$,$\therefore \angle DOB = \angle AOB + \angle AOD = 90^{\circ} + 60^{\circ} = 150^{\circ}$.
(2)分两种情况:①当OC在OA的右侧时,如答图1,$\because \angle AOD = 5\angle AOC$,$\because \angle AOD + \angle AOC = 90^{\circ}$,$\therefore \angle AOD = 90^{\circ} × \frac{5}{6} = 75^{\circ}$,$\therefore \angle DOB = \angle AOD + \angle AOB = 75^{\circ} + 90^{\circ} = 165^{\circ}$;②当OC在OA的左侧时,如答图2,$\because \angle AOD = 5\angle AOC$,$\therefore \angle COD = 4\angle AOC$,$\because \angle COD = 90^{\circ}$,$\therefore \angle AOC = \frac{1}{4}\angle COD = \frac{1}{4} × 90^{\circ} = 22.5^{\circ}$,$\therefore \angle DOB = 360^{\circ} - (\angle COD + \angle AOC + \angle AOB) = 360^{\circ} - (90^{\circ} + 22.5^{\circ} + 90^{\circ}) = 157.5^{\circ}$.
综上所述,$\angle DOB$的度数为$165^{\circ}$或$157.5^{\circ}$.


(3)分四种情况:①当OD在$\angle AOE$的内部时,如答图3,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOD + \angle AOC = n\angle AON + n\angle AOM = n\angle MON$,$\because \angle AOD + \angle AOC = \angle COD = 90^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 90 = 63n$,解得$n = \frac{10}{7}$;②当OC在$\angle AOE$的内部时,如答图4,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOD - \angle AOC = n\angle AON - n\angle AOM = n\angle MON$,$\because \angle AOD - \angle AOC = \angle COD = 90^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 90 = 63n$,解得$n = \frac{10}{7}$;③当OC,OD均在EF的下方时,如答图5,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOD + \angle AOC = n\angle AON + n\angle AOM = n\angle MON$,$\because \angle AOD + \angle AOC = 360^{\circ} - \angle COD = 360^{\circ} - 90^{\circ} = 270^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 270 = 63n$,解得$n = \frac{30}{7}$;④当OD在$\angle AOB$的内部时,如答图6,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOC - \angle AOD = n\angle AOM - n\angle AON = n\angle MON$,$\because \angle AOC - \angle AOD = \angle COD = 90^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 90 = 63n$,解得$n = \frac{10}{7}$.
综上所述,$n$的值为$\frac{10}{7}$或$\frac{30}{7}$.




23.解:
(1)由题意得$\angle AOB = \angle COD = 90^{\circ}$,$\because \angle AOC = 30^{\circ}$,$\therefore \angle AOD = \angle COD - \angle AOC = 90^{\circ} - 30^{\circ} = 60^{\circ}$,$\therefore \angle DOB = \angle AOB + \angle AOD = 90^{\circ} + 60^{\circ} = 150^{\circ}$.
(2)分两种情况:①当OC在OA的右侧时,如答图1,$\because \angle AOD = 5\angle AOC$,$\because \angle AOD + \angle AOC = 90^{\circ}$,$\therefore \angle AOD = 90^{\circ} × \frac{5}{6} = 75^{\circ}$,$\therefore \angle DOB = \angle AOD + \angle AOB = 75^{\circ} + 90^{\circ} = 165^{\circ}$;②当OC在OA的左侧时,如答图2,$\because \angle AOD = 5\angle AOC$,$\therefore \angle COD = 4\angle AOC$,$\because \angle COD = 90^{\circ}$,$\therefore \angle AOC = \frac{1}{4}\angle COD = \frac{1}{4} × 90^{\circ} = 22.5^{\circ}$,$\therefore \angle DOB = 360^{\circ} - (\angle COD + \angle AOC + \angle AOB) = 360^{\circ} - (90^{\circ} + 22.5^{\circ} + 90^{\circ}) = 157.5^{\circ}$.
综上所述,$\angle DOB$的度数为$165^{\circ}$或$157.5^{\circ}$.


(3)分四种情况:①当OD在$\angle AOE$的内部时,如答图3,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOD + \angle AOC = n\angle AON + n\angle AOM = n\angle MON$,$\because \angle AOD + \angle AOC = \angle COD = 90^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 90 = 63n$,解得$n = \frac{10}{7}$;②当OC在$\angle AOE$的内部时,如答图4,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOD - \angle AOC = n\angle AON - n\angle AOM = n\angle MON$,$\because \angle AOD - \angle AOC = \angle COD = 90^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 90 = 63n$,解得$n = \frac{10}{7}$;③当OC,OD均在EF的下方时,如答图5,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOD + \angle AOC = n\angle AON + n\angle AOM = n\angle MON$,$\because \angle AOD + \angle AOC = 360^{\circ} - \angle COD = 360^{\circ} - 90^{\circ} = 270^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 270 = 63n$,解得$n = \frac{30}{7}$;④当OD在$\angle AOB$的内部时,如答图6,$\because \angle AOD = n\angle AON$,$\angle AOC = n\angle AOM$,$\therefore \angle AOC - \angle AOD = n\angle AOM - n\angle AON = n\angle MON$,$\because \angle AOC - \angle AOD = \angle COD = 90^{\circ}$,$\angle MON = 63^{\circ}$,$\therefore 90 = 63n$,解得$n = \frac{10}{7}$.
综上所述,$n$的值为$\frac{10}{7}$或$\frac{30}{7}$.




查看更多完整答案,请扫码查看


