《2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版》

23. (13 分)(丹东东港期末)
【创设情境】
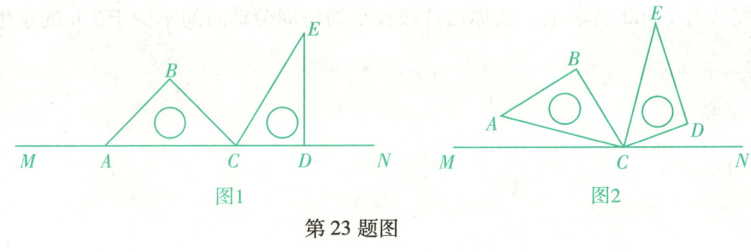
在数学活动课上，老师带领学生用一副直角三角尺进行“玩转三角尺”的探究活动.
(1)老师将三角尺$ABC$和三角尺$CDE$按如图 1 所示的方式摆放在直线$MN$上，边$AC$，$CD$落在直线$MN$上，$\angle ABC = \angle CDE = 90^{\circ}$，$\angle ACB = 45^{\circ}$，$\angle DCE = 60^{\circ}$，则$\angle BCE$的度数为75°.
【实践探究】
(2)第一小组将图 1 中三角尺$CDE$绕点$C$按逆时针方向旋转进行探究，当边$CD$首次落在直线$MN$上时停止旋转. 若以每秒$25^{\circ}$的速度旋转，设三角尺$CDE$的旋转时间为$t$秒，提出下列问题，请你解答.
①当$t = $3秒时，边$CE$落在边$BC$上.
②当$CD$平分$\angle ACB$时，$t = $6.3秒.
【深度探究】
(3)如图 2，第二小组受第一小组的启发继续进行探究：在三角尺$CDE$绕点$C$以每秒$20^{\circ}$的速度按逆时针方向旋转的同时，三角尺$ABC$也绕点$C$以每秒$4^{\circ}$的速度按顺时针方向旋转，当三角尺$CDE$的边$CD$首次落在直线$MN$上时停止旋转，同时三角尺$ABC$也停止旋转. 请直接写出$t$为何值时，$\angle BCE = 15^{\circ}$.

答案：
23.解：
(1)$75^{\circ}$ [解析]$\because \angle ACB+\angle BCE+\angle DCE = 180^{\circ}$，$\angle ACB = 45^{\circ}$，$\angle DCE = 60^{\circ}$，$\therefore \angle BCE = 180^{\circ}-\angle ACB-\angle DCE = 75^{\circ}$.
(2)①$3$ [解析]边$CE$旋转落在边$BC$上时，其旋转角$\angle BCE = 75^{\circ}$，$\because CE$的旋转速度为每秒$25^{\circ}$，$\therefore t = 75 ÷ 25 = 3(秒)$.
②$6.3$ [解析]如答图，作$CF$平分$\angle ACB$，$\because \angle ACB = 45^{\circ}$，$\therefore \angle BCF=\frac{1}{2}\angle ACB = 22.5^{\circ}$，$\therefore \angle DCF = \angle DCE+\angle ECB+\angle BCF = 60^{\circ}+75^{\circ}+22.5^{\circ}=157.5^{\circ}$，当$CD$旋转到$CF$时，旋转了$157.5^{\circ}$，$\because CD$的旋转速度为每秒$25^{\circ}$，$\therefore t = 157.5 ÷ 25 = 6.3(秒)$.

(3)由
(1)知两个三角尺旋转前$\angle BCE = 75^{\circ}$，设各三角尺都旋转了$t$秒，此时边$BC$旋转了$(4t)^{\circ}$，边$EC$旋转了$(20t)^{\circ}$.分两种情况：①当边$BC$与边$EC$相遇前$\angle BCE = 15^{\circ}$，有$4t + 20t = 75 - 15$，解得$t = 2.5$；②当边$BC$与边$EC$相遇后$\angle BCE = 15^{\circ}$，有$4t + 20t = 75 + 15$，解得$t = 3.75$.
综上所述，$t$为$2.5$秒或$3.75$秒时，$\angle BCE = 15^{\circ}$.